У вікні готових результатів буде видана таблиця, яка приведена далі. У ній будуть відображені основні і проміжні показники критерію Колмогорова - Смирнова. Основний показник, тобто власне величина критерію розташована в таблиці на рядку «Most Extreme Differences Absolute» (абсолютне максимальне розбіжність експериментальної кривої з кривою нормального розподілу). В даному прикладі вона склала D = 0,175.
One-Sample Kolmogorov-Smirnov Test
a. Test distribution is Normal. b. Calculated from data.
Щоб правильно проінтерпретувати отриману величину критерію. необхідно порівняти це значення з критичним значенням, встановленим для даного критерію. Критичне значення береться з спеціальної таблиці, яку можна знайти в підручниках за статистикою.
Коротко можна сказати, що для вибору потрібного критичного значення необхідно взяти рядок, яка відповідає кількості осіб в експериментальній вибірці за мінусом 1 (ця величина дорівнює ступеня свободи вибірки). Потім в розділі «Перевірка одиничної вибірки» знайти стовпець, де написано D0,05. після чого взяти значення, що стоїть на перетині з обраної рядком, - це і є те критичне значення критерію, з яким Ви повинні порівняти отримане в SPSS значення.
Наприклад, число членів Вашої вибірки (N) склало 36, як зазначено в наведеній вище таблиці. Отже, ступінь свободи вибірки дорівнює: 36-1 = 35, значить повинна бути обрана рядок, де вказано число 35. Далі дивимося, чому відповідає критичне значення критерію для D0,05. воно виявилося рівним 0,230. Порівнявши експериментальне значення критерію (0,175) з критичним значенням (0,230), ми бачимо, що воно не перевищило останнім, з чого робиться висновок про відсутність достовірних відмінностей між експериментальним розподілом даних і нормальним розподілом. Якщо ж експериментальне значення виявилося б рівним або більше, ніж критичне значення, то висновок був би іншим: наявне розподіл достовірно відрізняється від нормального розподілу.
Існує ще один дуже популярний спосіб оцінки достовірності відмінностей між розподілами або якимись групами даних - він стосується такого показника, як «рівень значущості». Даний показник є надзвичайно важливим показником для всіх методів статистики, тому вміння його інтерпретувати дає ключ до розуміння суті результатів будь-статистичної обробки даних!
Якщо викласти суть показника «рівня значущості» коротко, то можна сказати, що він показує те, наскільки можна довіряти висновку про наявність достовірних відмінностей, іншими словами, наскільки помилковим може виявитися такий висновок. Якщо помилковість висновку становить всього 5%, це означає, що тільки 5% даних не підтверджують гіпотезу про наявність достовірних відмінностей, а решта 95% даних свідчать на користь наявності достовірних відмінностей між розподілами або групами даних. При такому розкладі даних цілком можливо прийняти гіпотезу про наявність відмінностей і визнати її достовірною, тобто надійної.
Рівень значущості (достовірності) гіпотези зазвичай позначається в книгах по статистиці буквою «р» (це скорочення від слова «probability» - «ймовірність» помилки у висновку, тобто величина зворотна ступеня надійності виведення).
Але в статистичних пакетах рівень значимості прийнято позначати трьома буквами «sig» (це скорочення від слова «significance» - «значимість», тобто «вагомість», обґрунтованість висновку). Величина рівня значущості виражається зазвичай не у відсотках, а в частках від цілого (від одиниці): наприклад, п'яти відсотковий рівень помилковості висновку буде позначатися як sig = 0,05, що відповідає р = 0,05.
Ще краще, коли рівень помилковості виявляється рівним sig = 0,01, що вказує на 1% даних, які не узгоджуються з гіпотезою про наявність достовірних відмінностей, при цьому 99% даних підтверджують цю гіпотезу, отже, висновок про достовірних відмінностях буде дуже надійним або , як кажуть, високо достовірним.
У тих випадках, коли розрахований в SPSS показник рівня значущості (Sig) становить р> 0,05, тоді можна робити висновок про наявність достовірних відмінностей між порівнюваними розподілами або групами даних.
Вирішальне правило при побудові виведення про достовірність відмінностей можна виразити таким чином:
У розглянутому вище прикладі величина Sig, зазначена в самій нижній частині таблиці, виявилася на рівні 0,22, що перевищує величину 0,05 (р> 0,05), отже необхідно зробити висновок про відсутність достовірних відмінностей між отриманими в експерименті розподілом і нормальним розподілом даних. Іншими словами, отримане розподіл досить близько до нормальному розподілу.
Як бачимо, висновок, зроблений за показником рівня значущості, збігається з висновком, зробленим на основі порівняння величин самого критерію (розрахованого в SPSS та критичного значення з таблиці).
Щоб переконатися в правильності зроблених висновків, можна побудувати частотний розподіл експериментальних даних, які є в базі даних. Для цього потрібно повернутися до таблиці бази даних (через вкладку SPSS в панелі завдань) і вибрати команду «Graphs». Далі вибрати рядок «Chart Builder», після чого відкриється вікно, де потрібно задати характеристики для побудови графіка.
Вибір характеристик для побудови графіка частотного розподілу даних
У рубриці «Choose from» потрібно вибрати рядок зі словом «Histogram». Після цього з'являться маленькі картинки (зразки) побудови гістограм. Слід вибрати, наприклад, перший малюнок-зразок і натиснути на нього два рази. При побудові простого частотного розподілу на правому полі у вікні «Statistic» вибирається «Frequency Percent». Після вибору курсором цього рядка обов'язково натискається кнопка «Apply» в нижній частині цього поля, що призводить до появи даної характеристики на осі ординат в вікні умовного графіка. Тільки тепер можна натиснути на кнопку «ОК» для реального побудови графіка.
Відкривається вікно «Output» з побудованим графіком (якщо не відкривається, то викликати його через вкладку SPSS в панелі завдань).
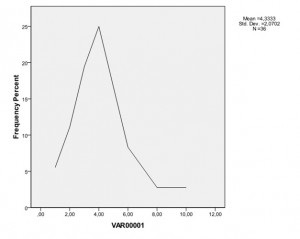
Крива частотного розподілу даних (частота народження результатів виражена просто у відсотках)
З графіка видно, що найбільш часто (на рівні 25-20%) зустрічаються середні величини, що відповідають значенням результатів в діапазоні від 3 до 6 одиниць. А крайні значення, такі як 1-2 або 7-10 зустрічаються з частотою на рівні 7-5%. Отже, в цьому розподілі частота народження середніх за величиною значення явно домінує над частотою народження крайніх значень (низьких і високих). Це вказує на те, що дане розподіл носить характер досить близький до нормального, який показаний на малюнку.
Крива нормального розподілу частоти виникнення даних (результатів тесту) у вибірці випробовуваних
Таким чином, число наочно вдалося перевірити висновок про те, що отримане в експерименті розподіл не має достовірних відмінностей від нормального розподілу, а навпаки, досить близько до нього за своїм характером. Розподіл, відмінне від нормального, зовсім іншого роду.
Крива аномальних розподілу даних по частоті
Достовірно відрізнятися від нормального розподілу буде такий розподіл даних, де крайні результати зустрічається набагато частіше, ніж середні значення, як це показано на малюнку.
Якщо в області середніх значень спостерігається «провал» і при цьому присутні два «горба» по краях, то така конфігурація кривої може означати, що вибірка не є гомогенною за своїм складом, тобто в ній об'єднані дві підгрупи людей, які істотно різняться між собою по досліджуваному ознакою, що і призводить до появи двох піків в розподілі даних.