Визначення внутрішніх зусиль ферми
Найчастіше у нас немає можливості застосувати звичайну балку для того чи іншого будови, і ми змушені застосовувати більш складну конструкцію, яка називається ферма.
Розрахунок металевої ферми хоч і відрізняється від розрахунку балки, але нам не важко буде її розрахувати. Від вас буде вимагатися лише увагу, початкові знання алгебри і геометрії і годину-дві вільного часу.
Тож почнемо. Перед тим, як розраховувати ферму, давайте поставимо собі який-небудь реальною ситуацією, з якою ви б могли зіткнутися. Наприклад, вам необхідно перекрити гараж шириною 6 метрів і довжиною 9 метрів, але ні плит перекриття, ні балок у вас немає. Тільки металеві куточки різних профілів. Ось з них ми і будемо збирати нашу ферму!
В подальшому на ферму будуть спиратися прогони і профнастил. Спирається ферми на стіни гаража - шарнірне.
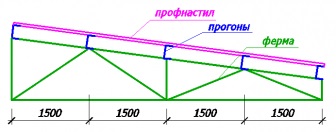
Для початку вам необхідно буде дізнатися все геометричні розміри і кути вашої ферми. Тут нам і знадобиться наша математика, а саме - геометрія. Кути знаходимо за допомогою теореми косинусів.
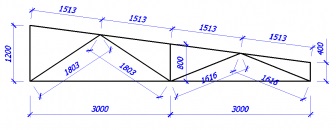
Потім потрібно зібрати всі навантаження на вашу ферму (подивитися можна в статті Розрахунок навісу). Нехай у вас вийшов такий варіант завантаження:
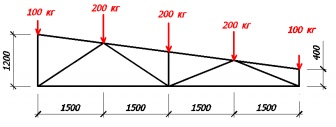
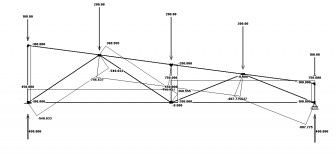
Далі нам потрібно пронумерувати всі елементи, вузли ферми і задати опорні реакції (елементи підписані зеленим, а вузли блакитним).
Щоб знайти наші реакції, запишемо рівняння рівноваги зусиль на вісь y і рівняння рівноваги моментів щодо вузла 2.
З другого рівняння знаходимо опорну реакцію Rb:
Rb = (200 * 1,5 + 200 * 3 + 200 * 4,5 + 100 * 6) / 6;
Rb = 400 кг
Знаючи, що Rb = 400 кг, з 1-ого рівняння знаходимо Ra:
Після того, як опорні реакції відомі, ми повинні знайти вузол, де найменше невідомих величин (кожен пронумерований елемент - це невідома величина). З цього моменту ми починаємо розділяти ферму на окремі вузли і знаходити внутрішні зусилля стрижнів ферми в кожному з цих вузлів. Саме за цими внутрішнім зусиллям ми і будемо підбирати перетину наших стрижнів.
Якщо вийшло так, що зусилля в стержні спрямовані від центру, значить наш стрижень прагне розтягнутися (повернутися в початкове положення), а значить сам він стиснутий. А якщо зусилля стержня спрямовані до центру, значить стрижень прагне стиснутися, тобто він розтягнутий.
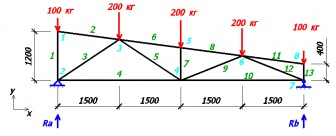
Отже, перейдемо до розрахунку. У вузлі 1 всього 2 невідомих величини, тому розглянемо цей вузол (спрямування зусиль S1 і S2 задаємо зі своїх міркувань, в будь-якому випадку у нас за підсумком вийде правильно).
Розглянемо рівняння рівноваги на осі х і у.
S2 * sin82,41 = 0; - на вісь х
-100 + S1 = 0; - на вісь y
З 1-ого рівняння видно, що S2 = 0, тобто 2-ий стрижень у нас не завантажений!
З 2-ої рівняння видно, що S1 = 100 кг.
Оскільки значення S1 у нас вийшло позитивним, значить напрямок зусилля ми вибрали правильно! Якщо ж воно б вийшло негативним, то напрямок варто поміняти і знак змінити на «+».
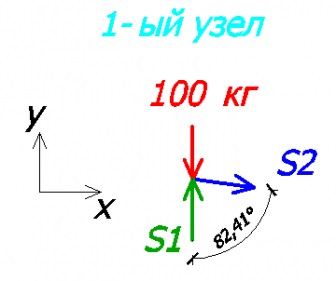
Знаючи напрямок зусилля S1, ми можемо уявити, що з себе представляє 1-ий стрижень.
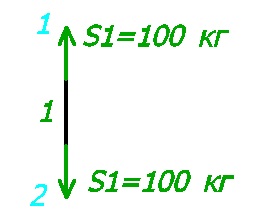
Оскільки одне зусилля було направлено в вузол (вузол 1), то і друге зусилля буде спрямовано в вузол (вузол 2). Значить наш стрижень намагається розтягнутися, а значить він стиснутий.
Далі розглянемо вузол 2. У ньому було 3 невідомих величини, але оскільки ми вже знайшли значення і напрямок S1, то залишається тільки 2 невідомих величини.
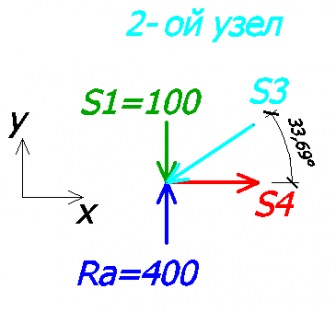
Знову ж складемо рівняння на осі х і у:
-100 + 400 - sin33,69 * S3 = 0 - на вісь у
- S3 * cos33,69 + S4 = 0 - на вісь х
З 1-ого рівняння S3 = 540,83 кг (стрижень №3 стиснутий).
З 2-ої рівняння S4 = 450 кг (стрижень №4 розтягнутий).
Розглянемо 8-ий вузол:
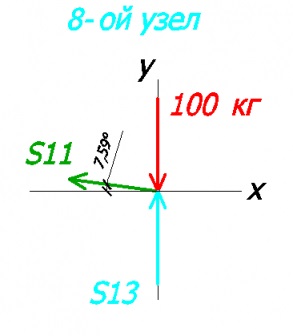
Складемо рівняння на осі х і у:
-100 + S13 = 0 - на вісь у
-S11 * cos7,59 = 0 - на вісь х
S13 = 100 кг (стрижень №13 стиснутий)
S11 = 0 (нульовий стрижень, ніяких зусиль в ньому немає)
Розглянемо 7-ий вузол:
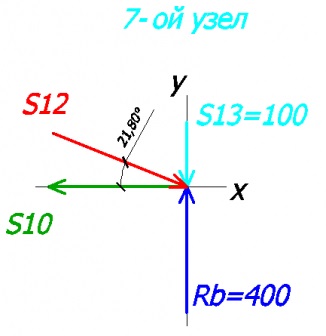
Складемо рівняння на осі х і у:
-100 + 400 - S12 * sin21,8 = 0 - на вісь у
S12 * cos21,8 + S10 = 0 - на вісь х
З 1-ого рівняння знаходимо S12:
S12 = 807,82 кг (стрижень №12 стиснутий)
З 2-ої рівняння знаходимо S10:
S10 = 750,05 кг (стрижень №10 розтягнутий)
Далі розглянемо вузол №3. Наскільки ми пам'ятаємо 2-ий стрижень у нас нульовою, а значить малювати його не будемо.
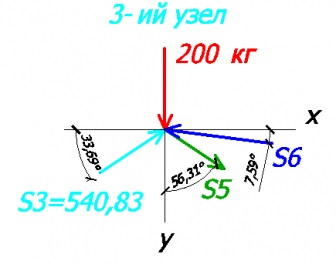
Рівняння на осі х і у:
-200 + 540,83 * sin33,69 - S5 * cos56,31 + S6 * sin7,59 = 0 - на вісь y
540,83 * cos33,69 - S6 * cos7,59 + S5 * sin56,31 = 0 - на вісь х
А тут нам уже знадобиться алгебра. Я не буду детально розписувати методику знаходження невідомих величин, але суть така - з 1-ого рівняння висловлюємо S5 і підставляємо її у 2-е рівняння.
За підсумком отримаємо:
S5 = 360,56 кг (стрижень №5 розтягнутий)
S6 = 756,64 кг (стрижень №6 стиснутий)
Розглянемо вузол №6:
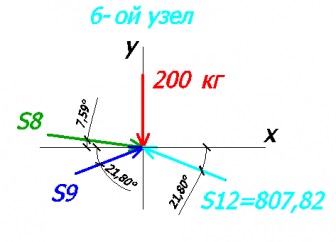
Складемо рівняння на осі х і у:
-200 - S8 * sin7,59 + S9 * sin21,8 + 807,82 * sin21,8 = 0 - на вісь у
S8 * cos7,59 + S9 * cos21,8 - 807,82 * cos21,8 = 0 - на вісь х
Так само, як і в 3-му вузлі знайдемо наші невідомі.
S8 = 756,64 кг (стрижень №8 стиснутий)
S9 = 0 кг (стрижень №9 нульовий)
Розглянемо вузол №5:
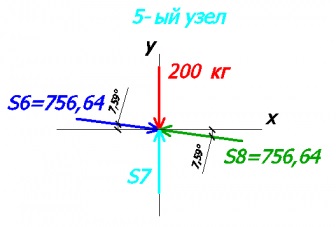
-200 + S7 - 756,64 * sin7,59 + 756,64 * sin7,59 = 0 - на вісь у
756,64 * cos7,59 - 756,64 * cos7,59 = 0 - на вісь х
З 1-ого рівняння знаходимо S7:
S7 = 200 кг (стрижень №7 стиснутий)
Як перевірки наших розрахунків розглянемо 4-ий вузол (зусиль в стержні №9 нету):
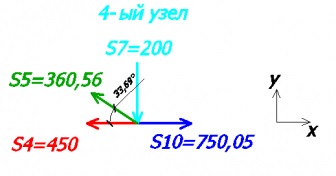
Складемо рівняння на осі х і у:
-200 + 360,56 * sin33,69 = 0 - на вісь у
-360,56 * cos33,69 - 450 + 750,05 = 0 - на вісь х
У 1-му рівнянні виходить:
У 2-му рівнянні:
Дана похибка допустима і пов'язана швидше за все з кутами (2 знака після коми замість 3-ох).
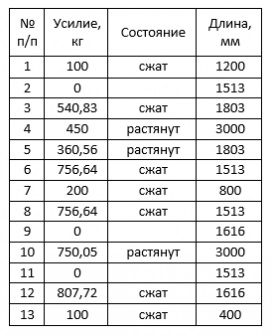
За підсумком у нас вийдуть наступні значення:
Вирішив перевірити ще раз всі наші розрахунки в програмі і отримав точно такі ж значення:
Підбір перерізу елементів ферми
При розрахунку металевої ферми після того, як всі внутрішні зусилля в стрижнях знайдені, ми можемо приступати до підбору перетину наших стрижнів.
Для зручності всі значення зведемо в таблицю.
Для розрахунків нам знадобиться не фактична довжина, а розрахункова. Розрахункову довжину ми зможемо знайти в СНиП II-23-81 * «Сталеві конструкції». Таблиця наведена нижче:
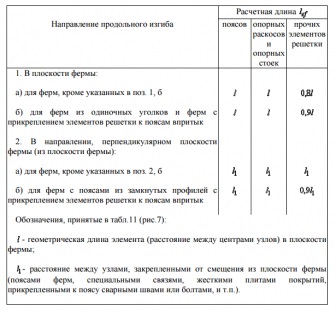
Як видно з таблиці, ми будемо перевіряти стрижень ферми в двох напрямках:
- в площині ферми
- з площини ферми (перпендикулярно площині ферми)
При довжині гаража в 9 метрів ми поставимо 4 ферми через 3 метри, а значить геометрична і розрахункова довжина стрижнів з площини ферми буде 3 метри.
Далі, в залежності від того стиснутий стрижень чи ні, по формулі ми розраховуємо необхідну площу поперечного перерізу.
При розрахунку стиснутих стержнів ми користуємося формулою (необхідна площа стержня):
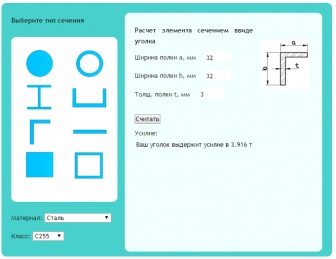
За цією формулою можна розрахувати в цьому онлайн розрахунку.
А також перевіряємо наш стрижень на максимальну гнучкість. Як правило, максимальна гнучкість не повинна бути більше 100-150.
Де lx - розрахункова довжина в площині ферми
Ly - розрахункова довжина з площини ферми
Ix - радіус інерції перерізу уздовж осі х
Iy - радіус інерції перерізу уздовж осі у
При розрахунку розтягнутих стрижнів ми користуємося такою формулою (необхідна площа стержня):
Цією формулою можна скористатися в онлайн розрахунку розтягнутих елементів.
Наприклад, два спарених куточка 32х3 витримають зусилля рівне 3.916 * 2 = 7,832 т.