Шевченко Л.В. старший викладач кафедри фізики
Донецький національний технічний університет
Моделювання фізичних процесів
Мета даної роботи - практично перевірити теоретичні знання про математичному маятнику. Для цього скористаємося побудовою комп'ютерної моделі математичного маятника. Фактично, ми проводимо пасивний обчислювальний експеримент.
Представлена модель математичного маятника створена в програмному комплексі MatLab / Simulink. Модель описує найпростіший варіант математичного маятника, в якому тіло підвішене на нерастяжимой нитки і коливання в системі незгасаючі.
Перш ніж описувати математичними формулами модель маятника, потрібно представити як виглядає досліджуване тіло. На малюнку 1 показаний досліджуваний маятник.
В даний момент тіло, підвішене на нерастяжимой нитки довгою. відхилено на деякий кут від положення вертикалі. Легко знайти складові кута відхилення.
Надалі, при побудові моделі математичного маятника будемо використовувати замість грецького позначення кута поєднання. Це пов'язано з тим, що при проектуванні моделі в системі моделювання можна користуватися грецькими буквами.
Для зручності, візьмемо нитка довжиною 1 метр. тоді:
Перед тим як приступити безпосередньо до моделювання, нам потрібно описати поведінку математичного маятника. У цьому полягає основна відмінність пасивного обчислювального експерименту від активного. У даній роботі ми працюємо з моделлю, всі необхідні властивості якої вже відомі заздалегідь [4].
Наведемо рух маятника. Як відомо, рівняння руху математичного маятника має вигляд:
де - кут відхилення маятника від положення рівноваги. Але в такій формі, рівняння не влаштовує нас. Знайдемо з рівняння кут:
В даному рівнянні ми бачимо залежність зміни кута відхилення маятника з плином часу. Тепер, після того, як у нас є рівняння, що описують руху маятника, можна приступити до створення програмної моделі. В системі моделювання Simulink. всі моделі будуються з блоків, які з'єднуються між собою сполучними лініями [1, 2]. Готова модель показана на малюнку 2.
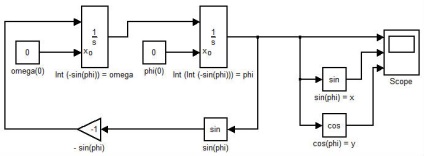
Кожен блок моделі підписаний:
- зміна знака надходить вираження на протилежний;
- блок тригонометричних функцій (.. І т.д.);
На схемі видно, що процес обчислення нового значення кута відхилення ітератівен. Сама схема умовно розділена на 2 частини (див. Рис. 3): частину обчислення значення кута і частина виведення результатів моделювання в якості графіка.
При отриманні нового значення кута. результати надходять на блок візуалізації. який за отриманими значеннями будує графіки залежності зміни кута від часу.
Після складання схеми моделі, потрібно запустити процес моделювання натисканням на кнопку:
Після завершення процесу симуляції, результати роботи можна побачити в блоці візуалізації (див. Рис. 4) [3].
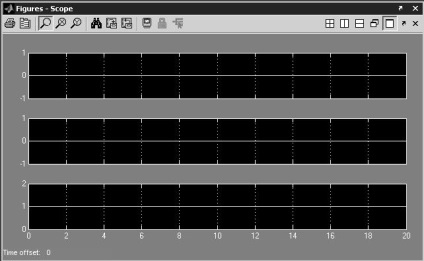
Як видно з малюнка 4, графіком коливань математичного маятника в такому випадку є пряма лінія. Іншими словами положення маятника протягом усього часу не змінюється. У чому ж справа? Якщо поглянути на схему моделі, то видно, що на інтегратори подаються початкові умови (кутова швидкість) і. Значить, потрібно зрушити маятник з місця. Зробити це можна або задавши початкову кутову швидкість відмінну від нуля, або початковий кут відхилення відмінний від нуля. Вибираючи між двома способами зміни положення маятника, будемо керуватися принципами наочності. І дійсно, процес відхилення і відпускання нитки з прив'язаним на кінці вантажем більш наочний, ніж процес надання швидкості тілу.
Змінимо початковий кут відхилення маятника, як показано на малюнку 5.
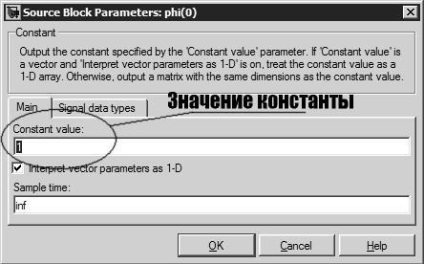
В системі Simulink кути задаються в радіанах. Зміни показані на малюнку 6.
Результатом симулювання буде графіки, зображені на малюнку 7.
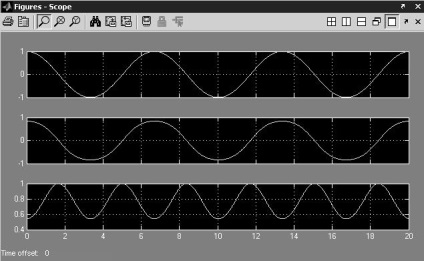
На трьох графіках показано зміна кута відхилення. горизонтальну складову руху і вертикальну складову руху. Для відображення результатів обраний авто масштаб.
Однак використання спеціалізованих середовищ моделювання не є єдино можливим шляхом моделювання поведінки маятника. Для здійснення завдання, можна було скористатися будь-якою мовою програмування і тоді б результати виводилися в тій формі, в якій побажав би програміст. Але такий підхід сильно ускладнює завдання і не дозволяє зосередитися тільки на процесі моделювання.
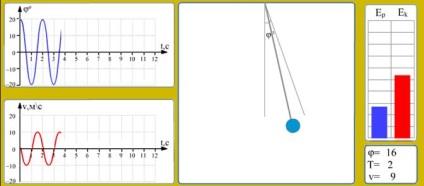
На малюнку 8-9 зображена демонстраційна програма моделювання математичного маятника в середовищі Macromedia Flash 6.0.
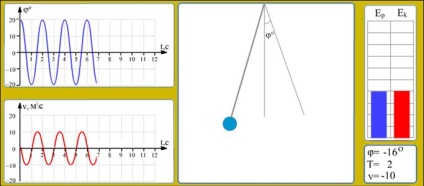
Дана модель демонструє процес гармонійних коливань математичного маятника. Виводяться графіки залежності кута відхилення від вертикалі і швидкості руху від часу. У вигляді змінюються діаграм показані значення кінетичної і потенційної енергій. У кожен момент часу показані значення кута відхилення і швидкості. Для розрахунків взяті такі значення: довжина нитки-1 метр, кут початкового відхилення - 20 градусів.