2.25. Секціонірованние згортки
У багатьох практичних завданнях необхідно обчислювати згортку двох кінцевих послідовностей, коли одна з них набагато довше іншої (скажімо, або). Звичайно, завжди можна вибрати рівним, але такий підхід неефективний і по ряду причин незручний. По-перше, перед обчисленням згортки потрібно мати всю довшу послідовність. На практиці, наприклад в радіолокації або при обробці мовних сигналів, ця умова не завжди здійснимо. По-друге, оскільки обробка починається тільки після прийому всієї послідовності, то результат виходить з великою затримкою. І нарешті, при дуже великих обчислення ДПФ значно ускладнюється, тому що для цього потрібен великий обсяг пам'яті і виникають деякі інші, чисто практичні труднощі, пов'язані з алгоритмами ШПФ. Від перерахованих недоліків вільні наступні два методи обчислення згортки. Вони засновані на розбитті довшою послідовності на секції і обчисленні часткових згорток, з яких потім формується шукана вихідна послідовність.
Перший з них називається методом перекриття з підсумовуванням. Сутність цього методу ілюструється на фіг. 2.32. Для простоти припустимо, що послідовність не обмежена, a містить відліків. Розділимо послідовність на суміжні секції довжиною по відліків (фіг. 2.32). Вибір досить складний, але хороші результати виходять, якщо є величиною того ж порядку, що і .Отже, вхідна послідовність представляється у вигляді
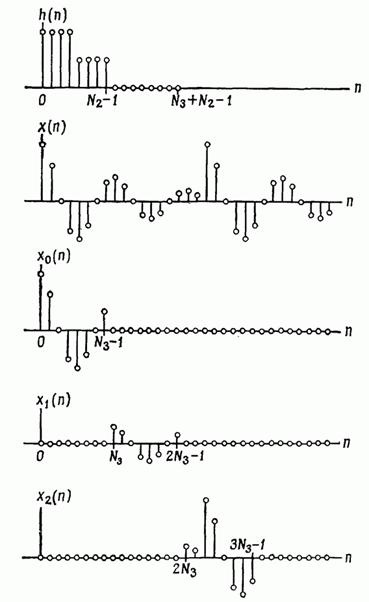
Фіг. 2.32. Метод перекриття з підсумовуванням.
Лінійна згортка послідовностей і дорівнює
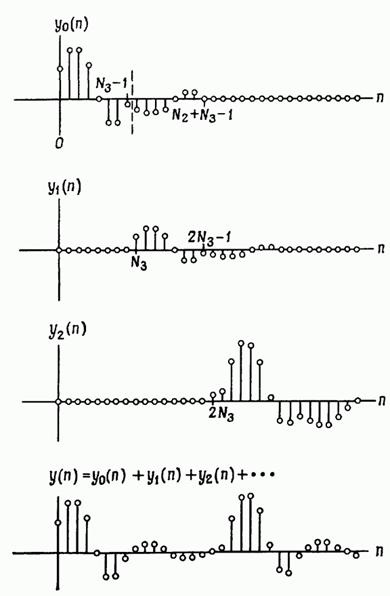
Фіг. 2.33. Формування вихідних значень згортки при використанні методу перекриття з підсумовуванням.
Довжина кожної з часткових згорток в сумі (2.169) дорівнює отсчетам, т. Е. Є ділянка довжиною в відліків, на якому -я і -я часткові згортки перекриваються, тому їх відліки на ділянці перекриття потрібно скласти. На фіг. 2.33 показано, як розташовані і як підсумовуються сусідні часткові згортки. Кожна з них обчислюється методом швидкої згортки, описаним в розд. 2.24. Розглянутий метод був названий методом перекриття з підсумовуванням саме тому, що проміжні часткові згортки перекриваються і для отримання кінцевого результату їх необхідно скласти.
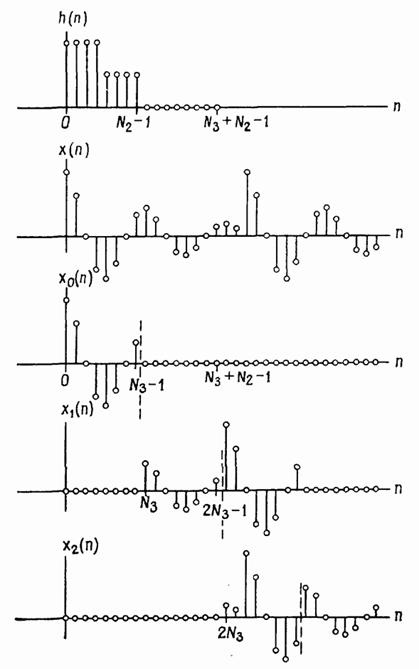
Фіг. 2.34. Метод перекриття з накопиченням.
Інший метод обчислення лінійної згортки послідовностей, одна з яких значно довша за іншу, також заснований на секціонуванні довшою послідовності. Його називають методом перекриття з накопиченням, причому в даному випадку перекриваються вхідні, а не вихідні секції. Помилкові відліки кругових згорток окремих секцій відкидаються. Решта відліки накопичуються і з них формується кінцевий результат. Розглянемо конкретний приклад (фіг. 2.34). Послідовність містить відліків, а послідовність розділена на секції довжиною по відліків, що перекриваються один з одним на ділянках довжиною по відліків. (Відзначимо, що ділянку перекриття знаходиться в кінці послідовності. Це зручно для обчислення кругової згортки за допомогою ДПФ.)
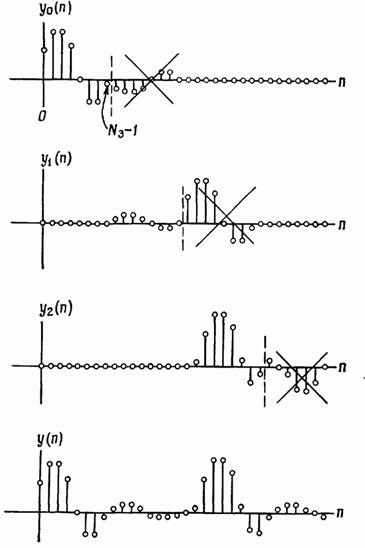
Фіг. 2.35. Формування вихідних значень згортки при використанні методу перекриття з накопиченням.
Для кожної секції обчислюється кругова згортки послідовностей і, що містить відлік. В результаті виходить набір послідовностей, зображених па фіг. 2.35. Останні відліків кожної з послідовностей відкидаються (вони невірні через циклічного характеру згортки), а інші приєднуються до правильних отсчетам послідовності і т. Д. В результаті виходить шукана послідовність, тотожна пакунку. Отже, використовуючи метод перекриття з підсумовуванням або метод перекриття з накопиченням, можна порівняно легко знайти згортку короткою і дуже довгою послідовностей, причому результат виходить у вигляді окремих невеликих секцій, які об'єднуються відповідним чином в одну послідовність.