Я теж хочу відповісти на цей специфічний питання, пов'язане з відкриттям засновником математичної логіки Д.Булем алгебри, названій на його честь. Булеву алгебру можна використовувати в курсі математичної логіки як модель досліджуваного класичного числення висловів. Хто вивчав це, той знає, що в цьому випадку 0 називають брехнею, 1 - істиною. Вирази, які містять булеві операції та змінні, - це і є висказивательной форми.
Зупинимося на необхідних визначеннях логіки висловлювань, які продемонструємо на прикладах.
Висловлення - це оповідної пропозицію, щодо якого можна сказати істинно воно або помилково.
А: Москва - столиця Росії - висловлювання, причому істинне.
В: 2 + 2 = 5 - це хибне висловлювання.
2 + 2 - це не вислів, тому що щодо його не можна сказати істинно воно або помилково.
Нас цікавлять не всі логічні операції, а тільки кон'юнкція (логічне множення), диз'юнкція (логічне додавання) і заперечення.
Кон'юнкція двох висловлювань називається нове висловлювання, що позначається А / \ В, справжнє тоді і тільки тоді, коли обидва висловлювання істинними.
Диз'юнкцією двох висловлювань називається складне висловлювання, що позначається А \ / В, помилкове тоді і тільки тоді, коли обидва висловлювання помилкові.
Запереченням висловлювання А називається висловлювання, що позначається / А (НЕ А), помилкове тоді і тільки тоді, коли саме висловлювання істинно.
Складемо кон'юнкцію, диз'юнкцію висловлювань А і В (див. Вище) і заперечення висловлювання А.
А / \ В: Москва-столиця Росії і 2 + 2 = 5 (відповідає союз і) - кон'юнкція помилкова (див. Третій рядок таблиці істинності для неї - 1,2,4 стовпці).
А \ / В: Москва - столиця Росії або 2 + 2 = 5 (відповідає союз або) - диз'юнкція істинна (див. Третій рядок таблиці істинності для неї - 1,2,5 стовпці).
/ А: Невірно, що Москва - столиця Росії (можна і так: Москва - не столиця Росії) (відповідає частка не) - заперечення помилкове (див. Третій рядок таблиці істинності для заперечення - 1,2,3 стовпці).
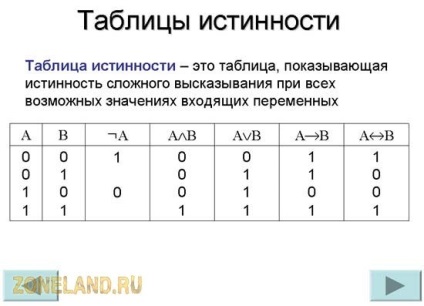
Нижче наведена зведена таблиця істинності, яка складена для всіх п'яти операцій (маються ще 2 операції: імплікація і еквіваленція, см. Шостий і сьомий стовпчики), але у визначенні булевої алгебри вони не беруть участь).
А тепер дамо точне визначення булевої алгебри (див. Тут).
Булевой алгеброю називається непорожня множина A з двома бінарними операціями / \ (аналог кон'юнкції), \ / (аналог диз'юнкції), унарною операцією / (аналог заперечення) і двома виділеними елементами: 0 (або Брехня) і 1 (або Істина) такими, що для будь-яких елементів з А a, b і c з безлічі A вірні такі аксіоми:
a / \ (b / \ c) = (a / \ b) / \ c a \ / (b \ / c) = (a \ / b) \ / c асоціативність
a / \ b = b / \ a a \ / b = b \ / a коммутативность
a / \ (a \ / b) = a a \ / (a / \ b) = a закони поглинання
a / \ (b \ / c) = (a / \ b) \ / (a / \ c) a \ / (b / \ c) = (a \ / b) / \ (a \ / c) дистрибутивность однієї операції щодо іншої
a \ / / a = 1 a / \ / a = 0 додатковість
Зауваження: бінарна операція пов'язує два елементи, унарна - один елемент.


Зазначу, що булева алгебра широко застосовується на практиці. Для зацікавлених пропоную подивитися ось цей барвистий матеріал .. в якому показано, що
А також розглянута алгебра лотки.
Булева алгебра це створена Джорджем Булем і вдосконалена рядом інших математиків система запису логічних виразів. Згодом вона виросла в важливий напрям науки - математичну логіку. Широко застосовується в програмуванні.
У булевої алгебри виділяють кілька видів операцій. Наприклад, операція заперечення може бути виражена "якщо вираз А істинно, то вираз Б помилково". Наприклад, якщо істинно вираз "поїзд прийде із запізненням", то помилково вираз "я встигну до початку фестивалю".
Операція складання (операнд І) полягає в тому, що є складне висловлювання, яке істинно тільки тоді, коли істинні обидва його частини. Наприклад, "якщо спектакль буде цікавим, то я не засну".
Логічне АБО означає вираз, вірне тоді, коли істинна чи одна входить в нього частину, або друга. Наприклад, "він встигне, якщо зловить таксі або зуміє завести мотоцикл".