Широкосмугові фільтри гармонік
науковий керівник д-р. техн. наук
В останні роки проблема забезпечення якості електроенергії, викликана широким поширенням нелінійних навантажень, що створюють при своїй роботі струми несинусоїдної форми, стала дуже значущою. Несинусоїдальні струми можна представити у вигляді суми гармонік, частоти яких кратні основній частоті живильної мережі. Вищі гармоніки надають несприятливий вплив на роботу електрообладнання.
Основним засобом придушення або ослаблення вищих гармонік, що генеруються нелінійним навантаженням, в системах електропостачання є активні і пасивні фільтри гармонік.
Уявімо систему фільтр - живить мережу еквівалентною схемою, показаної на рис. 1. Тут - комплексне опір мережі з боку шин, до яких приєднана нелінійна навантаження, - комплексне опір фільтра. Джерело гармонік моделюється джерелом струму.
Комплексні опору фільтра і мережі на рис. 1 утворюють дільник струму, коефіцієнти передачі якого:
Коефіцієнти і визначають розподіл струму k -й гармоніки між фільтром і зовнішньою мережею. Для коефіцієнтів розподілу справедливо рівність:
.
З формул (1) і (2) випливає, що на передачу струму k -й гармоніки в зовнішню мережу впливають не тільки характеристики фільтра, але і частотна характеристика мережі. Для ефективного придушення струму k -й гармоніки значення коефіцієнта на частоті цієї гармоніки має бути мінімальним.
У статті розглянута процедура проектування широкосмугових фільтрів гармонік, заснована на використанні методів реалізації LC -четирехполюсніков сходовій структури. Пропонований метод може бути використаний для розрахунку відомих структур Вовнопрядильна або для отримання нових конфігурацій таких фільтрів.
Пропонована процедура проектування широкосмугового фільтру включає три етапи. На першому етапі виконується розрахунок фільтра-прототипу нижніх частот, що має частоту зрізу, рівну 1 рад / с.
На другому етапі нормований НЧ-прототип трансформується в фільтр верхніх частот за допомогою частотного перетворення, що визначається виразом: s = wc / p. Тут - частота зрізу фільтра верхніх частот. При такому перетворенні передавальна функція ФНЧ-прототипу перетворюється в передавальну функцію ФВЧ з частотою зрізу. При цьому конденсатори замінюються котушками, індуктивність яких дорівнює Генрі. Котушки НЧ-прототипу замінюються конденсаторами ємністю фарад.
На третьому етапі проводиться денормирование опорів гілок фільтра верхніх частот для того, щоб забезпечити необхідну величину реактивної потужності на частоті першої гармоніки.
Передавальна функція фільтра, виражена через y -параметри чотириполюсника,
Завдання реалізації передавальної функції, яка визначається формулою (1), зводиться до одночасної реалізації параметрів і LC -четирехполюсніка.
З теорії синтезу пасивних ланцюгів відомо, що і - непарні раціональні функції комплексної змінної s. мають однаковий знаменник. позначимо:
Якщо - парний поліном, то і - непарні, і навпаки.
Підставивши вирази (4) в формулу (3), отримаємо:
.
Таким чином, знаменник дорівнює сумі поліномів, що утворюють чисельник і знаменник. Поліноми і необхідно вибрати так, щоб їх нулі розташовувалися на осі і чергувалися. У цьому випадку параметр буде функцією вхідної провідності LC -ланцюга.
Практичний інтерес представляють два випадки. У першому випадку все нулі передачі синтезованого фільтра розташовані на початку координат. У другому випадку передавальна функція фільтра має нуль на частоті основної гармоніки. Обмежимося розглядом випадку, коли нулі передачі НЧ-прототипу розташовані в нескінченності.
Передавальна функція має вигляд (для визначеності розглянемо фільтр третього порядку):
.
Тут ai - коефіцієнти полінома знаменника, які залежать від виду передавальної функції. Відповідно до формули (3):
; .
Для реалізації параметрів і доцільно використовувати сходову схему, показану на рис. 3. Значення елементів залежать від коефіцієнтів полінома знаменника.
Для ілюстрації пропонованої процедури розглянемо приклад розрахунку широкосмугового фільтру третього порядку,
призначеного для придушення гармонік з порядковими номерами
Виберемо як прототип фільтр нижніх частот Баттерворта. Нормована передавальна функція:
.
Оскільки чисельник - парний поліном, відповідно до (3) і (4) y -параметри LC -четирехполюсніка:
; .
Розкладаючи в безперервну дріб при, визначимо нормовані значення елементів в схемі на рис. 3: Гн, Ф, Гн. В теорії синтезу пасивних ланцюгів таку структуру називають першою канонічної схемою Кауера.
Для отримання фільтра верхніх частот використовуємо перетворення НЧ-ВЧ, яке визначається формулою (1). Частоту зрізу фільтра верхніх частот виберемо рівною частоті 10-й гармоніки: рад / с. В результаті перетворення отримаємо широкосмуговий фільтр (рис. 4).
Номінали елементів фільтра на рис. 4: мкФ, мГн, мкФ.
Аналогічним чином можна розрахувати параметри широкосмугових фільтрів, що реалізують різні передавальні функції. У табл. 1 і 2 наведені значення елементів нормованих НЧ-прототипів другого і третього порядків, які реалізують передавальні
функцій Баттерворта і Чебишева.
Таблиця 1. Значення елементів ФНЧ-прототипу 2 порядки
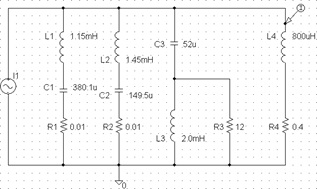
Як приклад розглянемо пасивне Фільтркомпенсуючий пристрій (рис. 5), що забезпечує компенсацію реактивної потужності і придушення гармонік, що генеруються нелінійним навантаженням. Такий навантаженням є трифазний мостовий випрямляч.
ФКУ є складовою фільтр гармонік, утворений двома резонансними і одним широкосмуговим ланками. Резонансні ланки фільтра призначені для придушення 5 і 7 гармонік. Широкосмугове ланка послаблює гармоніки з порядковими номерами.
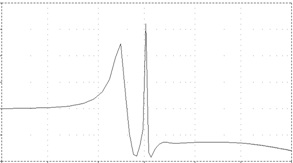
На рис. 6 показана амплітудно-частотна характеристика синтезованого фільтра, розрахована за допомогою програми Pspice.



Підпишіться на розсилку:

Цікаві новини
важливі теми
Огляди сервісів Pandia.ru