1. Гармонійне коливання.
Математична модель гармонійного коливання має вигляд:
u (t) = Ums sin (# 969; st + # 966; s) (11)
Як видно з математичної моделі, в спектрі цього коливання присутній одна гармонійна складова, яка знаходиться на частоті # 969; s. Висота складової в спектрі амплітуд дорівнює амплітуді коливання Ums, а в спектрі фаз - початковій фазі коливання # 966; s. Причому при побудові спектра необхідно враховувати зв'язок між тимчасової діаграмою сигналу і спектром амплітуд. Амплітуда складової спектра повинна по висоті відповідати амплітуді коливання на тимчасовій діаграмі.
Необхідно відзначити, що при збільшенні частоти сигналу, його складова буде віддалятися по осі частот від нуля (рисунок 13).
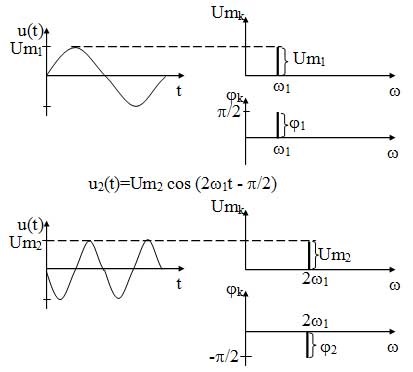
Малюнок 13 - Спектральний уявлення гармонійних коливань
Як видно з малюнків, спектр гармонійного коливання є дискретним і обмеженим.
2. Періодичні, негармонійні сигнали.
Основною особливістю спектрального уявлення таких сигналів є наявність в їх спектрі безлічі спектральних складових. Такі сигнали можуть бути описані рядом Фур'є, згідно з яким:
т. е. сигнал може бути представлений сумою постійної складової і безлічі гармонійних складових.
Перетворимо даний ряд, використовуючи тригонометрическое властивість
sin (x + y) = sin x cos y + cos x sin y (13)
Вважаючи що x = # 966; k і y = k # 969; ct отримаємо:
Оскільки Umk і # 966; k є параметрами ряду, то їх можна позначити коефіцієнтами
Umk sin # 966; k = ak; Umk cos # 966; k = bk (15)
Тоді ряд набуде вигляду:
Параметри ряду можна визначити через коефіцієнти ak і bk:
Амплітуда постійної складової і коефіцієнти можуть бути визначені через значення сигналу u (t):

З ряду випливає, що якщо описуваний сигнал є парною функцією f (t) = f (-t), то ряд буде мати тільки косинусоидальной складові, так як bk = 0, якщо непарна функція (f (t) ≠ f (-t) ), то радий містить тільки синусоїдальні складові (ak = 0).
Розглянемо спектральне подання періодичних, негармонійних сигналів на прикладі періодичної послідовності прямокутних імпульсів (ПППІ).
При побудові спектра необхідно розрахувати наступні параметри:
а) шпаруватість сигналу:
б) значення постійної складової:
в) частоту першої гармоніки спектра, яка дорівнює частоті сигналу:
г) амплітуди гармонійних складових спектру:
При побудові спектра необхідно відзначити такі особливості:
1. Всі гармонійні складові знаходяться на частотах, кратних частоті першої гармоніки (2 # 969; 1, 3 # 969; 1, 4 # 969; 1 і т. Д.);
2. Для спектра амплітуд:
а) спектр ПППІ має пелюстковий характер, т. е. в спектрі можна виділити безліч «пелюсток»;
б) кількість гармонійних складових в пелюстці залежить від шпаруватості і одно q - 1;
в) амплітуди гармонійних складових, що знаходяться на частотах, кратних скважности, дорівнюють нулю;
г) форма спектра позначається обвідної - пунктирною лінією, плавно з'єднує вершини гармонійних складових;
д) точка, з якої виходить огинає, дорівнює 2U0 або 2I0.
3. Для спектра фаз:
а) все гармонійні складові, на частотах, які не кратних скважности, мають однакову висоту, рівну π / 2 (90 °);
б) все гармонійні складові в одному пелюстці мають однаковий знак, а в сусідніх протилежний.
в) складові на частотах кратних скважности мають початкову фазу рівну нулю.
Спектри ПППІ при шпаруватості q = 3 представлені на малюнку 14.
Як видно з діаграм спектр ПППІ є дискретним і необмеженим. Тому за ширину спектра приймають діапазон частот, в межах якого знаходиться два перших пелюстки, т. К. В них міститься близько 95% енергії сигналу:
# 916; fs = 2 / # 964; і. (26)
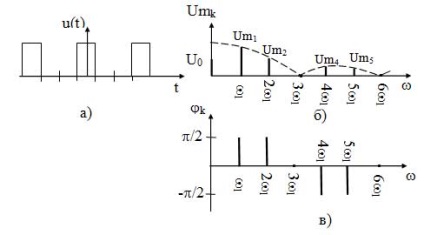
Малюнок 14 - Спектральний уявлення ПППІ: а) тимчасова діаграма; б) спектральна діаграма амплітуд; в) спектральна діаграма фаз
Як видно з формули ширина спектра ПППІ залежить тільки від тривалості імпульсу і не залежить від його періоду.
3. Непериодические сигнали.
Оскільки в неперіодичних сигналах можна виділити період, т. К. Т → ∞, то розрахувати і побудувати спектр тем же методом, що і для періодичних сигналів не можна. Однак знати спектр таких сигналів необхідно, т. К. Все інформаційні сигнали є непериодическими. Для побудови спектра непериодического сигналу виробляють наступну процедуру: сигнал подумки уявляють як періодичний з довільним періодом, ддля якого будують спектр. Потім здійснюють граничний перехід спрямовуючи період до нескінченності (Т → ∞) (рисунок 15). При цьому частота першої гармоніки і, відповідно, відстань між гармонійними складовими прагне до нуля (f1 = 1 / Т), тому всі складові зливаються один з одним і утворюють суцільний спектр.
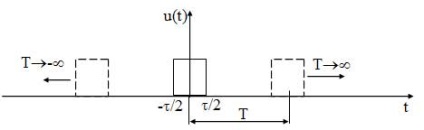
Малюнок 15 - Імпульсний сигнал u (t) і його уявлення періодичним сигналом
Форма спектра неперіодичних сигналів позначається обвідної (суцільною лінією) (рисунок 16).
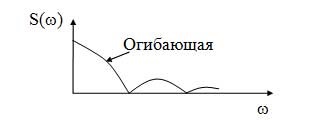
Малюнок 16 - Спектральна діаграма непериодического сигналу
Ряд Фур'є, для таких сигналів, також не можна записати, т. К. В цьому випадку амплітуда постійної складової і коефіцієнти ak і bk дорівнюють нулю. У цьому випадку значення сигналу в будь-який момент часу також дорівнює нулю, що є невірним. Тому для таких сигналів використовують перетворення Фур'є:
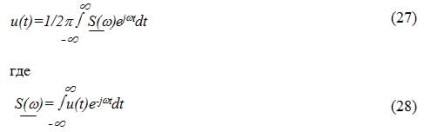
Вираз (27) є зворотним перетворенням, а (28) прямим перетворенням Фур'є.
Величина S (# 969;) є комплексною спектральної щільністю непериодического сигналу u (t). Вона дорівнює:
де S (# 969;) спектральна щільність амплітуд або амплітудний спектр непериодического сигналу, а # 966; (# 969;) - фазовий спектр непериодического сигналу.
Спектральна щільність амплітуд непериодического сигналу на будь-якій частоті # 969; дорівнює сумарній амплітуді складових знаходяться в малій смузі # 916; # 969; в околицях частоти # 969; перелічених на 1 Герц.
Тимчасові діаграми і спектральні щільності амплітуд для прямокутного і трикутного імпульсів представлені на малюнку 18:
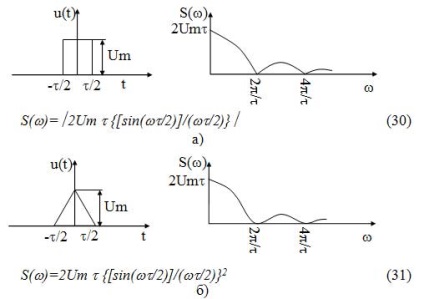
Малюнок 18 - Спектральний уявлення неперіодичних сигналів: а) прямокутний імпульс; б) трикутний імпульс