Тест Ярки-Бера на непротиворечие розподілу генеральної сукупності значень випадкової величини нормальному закону
H = jbtest (X)
H = jbtest (X, alpha)
[H, P, JBSTAT, CV] = jbtest (X, alpha)
H = jbtest (X) функція призначена для виконання тесту Ярки-Бера на непротиворечие розподілу генеральної сукупності значень слуайной величини нормальному закону по виборкеX.X задається як вектор. Функція повертає скалярH, що є результатом перевірки нульової гіпотези для критичного рівня значущості рівного 0,05. Нульова гіпотеза полягає в тому, що розподіл генеральної сукупності значень випадкової величини який суперечить нормальному закону. Альтернативна гіпотеза тесту Ярки-Бера полягає в тому, що розподіл генеральної сукупності суперечить нормальному закону. Нульова гіпотеза приймається якщо h = 0 при. ЕсліH = 1, то нульова гіпотеза може бути відкинута при.
Тест Ярки-Бера використовується у випадках, коли невідомі середнє арифметичне і дисперсія генеральної сукупності. Перевірка нульової гіпотези заснована на розрахунку оцінок коефіцієнтів асиметрії та ексцесу за вибіркою Х. У разі справедливості нульової гіпотези вибіркове значення коефіцієнта асиметрії має бути приблизно дорівнює нулю, а вибіркове значення ексцесу - трьом. Слід зазначити, що у вітчизняній літературі коефіцієнт ексцесу визначається за формулою, де - коефіцієнт ексцесу, - точкова оцінка середнього квадратичного відхилення, - четвертий емпіричний центральний момент, - вибіркове середнє арифметичне, - вектор вибіркових значень. Отже, коефіцієнт ексцесу нормального закону буде дорівнює 0.
При проведенні тесту Ярки-Бера визначаються відхилення вибіркових коефіцієнтів асиметрії та ексцесу, щодо очікуваних значень за умови справедливості нульової гіпотези для заданого обсягу вибірки. В якості запобіжного відхилень вибіркових значень коефіцієнтів асиметрії та ексцесу використовується статистика хі-квадрат. Тест Ярки-Бера використовується при великому обсязі вибірки Х. При малому обсязі вибірки використовується тест Лілліефорса.
H = jbtest (X, alpha) вхідний параметр alpha дозволяє задати значення критичного рівня значущості для перевірки нульової гіпотези. За умолчаніюalpha = 0,05. Умова прийняття нульової гіпотези
де - критичний рівень значимості; - рівень значущості, відповідний вибіркової статистики хі-квадрат. Вибір величини надано досліднику. У більшості практичних випадків приймають рівним 0,05; 0,01.
[H, P, JBSTAT, CV] = jbtest (X, alpha) вихідними параметрами функції є: 1. результат перевірки нульової гіпотези H для заданого критичного рівня значущості; 2. рівень значущості P, відповідний вибіркового значенням статистики хі-квадрат; 3. значення вибіркової статистики хі-квадратJBSTAT; 4. критичне значення статистики хі-квадратCV. ВелічінаCV служить для перевірки нульової гіпотези. якщо JBSTAT Приклади використання функції тесту Ярки-Бера на непротиворечие розподілу генеральної сукупності нормальному закону Тест Ярки-Бера на непротиворечие нормальному закону генеральної сукупності, розподіленої за нормальним законом, за вибірковими значеннями. Обсяг вибірки - 25 елементів. Функція повертає результат перевірки нульової гіпотези. Графічне представлення розподілу вибіркових значень виконується за допомогою функції histfit.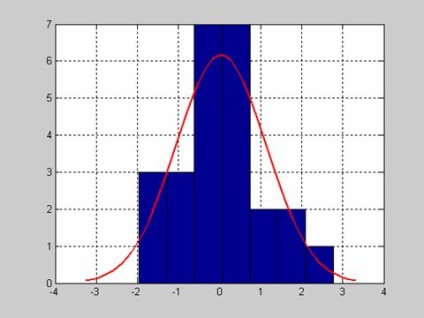
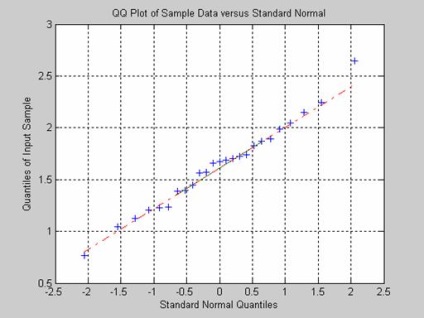
Тест Ярки-Бера на непротиворечие нормальному закону генеральної сукупності, розподіленої за нормальним законом, за вибірковими значеннями. Обсяг вибірки - 30 елементів. Функція повертає результат перевірки нульової гіпотези для критичного значення рівня значущості 0,01. Графічне представлення розподілу вибіркових значень виконується за допомогою функції> qqplot.
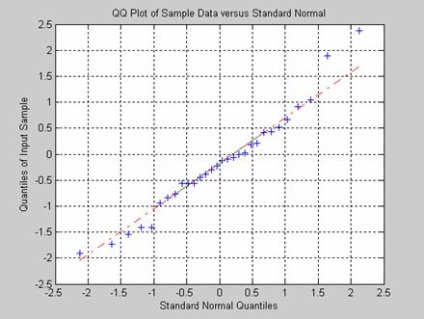
Тест Ярки-Бера на непротиворечие нормальному закону генеральної сукупності, розподіленої за нормальним законом, за вибірковими значеннями. Розподіл генеральної сукупності представляє композицію нормального і рівномірного законів. Обсяг вибірки - 30 елементів. Функція повертає результат перевірки нульової гіпотези для критичного рівня значущості 0,01. Графічне представлення розподілу вибіркових значень виконується за допомогою функції> qqplot.
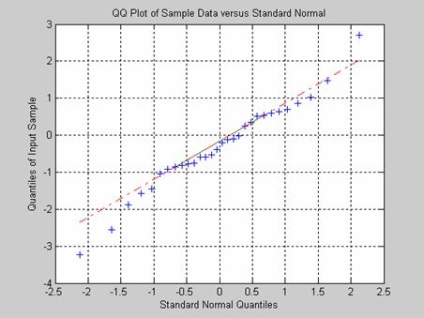
Тест Ярки-Бера на непротиворечие нормальному закону генеральної сукупності, розподіленої за нормальним законом, за вибірковими значеннями. Розподіл генеральної сукупності представляє композицію нормального і рівномірного законів. Обсяг вибірки - 30 елементів. Графічне представлення розподілу вибіркових значень виконується за допомогою функції> qqplot. Функція повертає результат перевірки нульової гіпотези для критичного рівня значущості 0,01; рівень значімостіP відповідний, вибіркового значенням статистики хі-квадрат; значення вибіркової тестової статистики хі-квадрат; критичне значення статистики хі-квадрат.
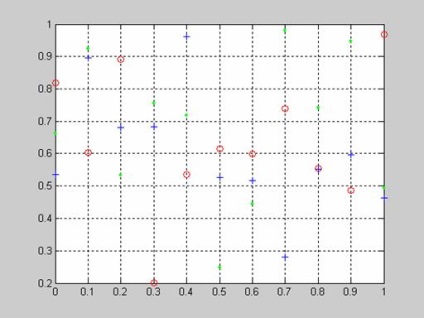
Залежність величини рівня значущості при перевірці нульової гіпотези від обсягу вибірки і дисперсії рівномірного закону, як складової композиції законів розподілу випадкової велічіниx. Розподіл генеральної сукупності є композицією нормального і рівномірного законів. Параметри нормальної складової постійні і рівні: математичне очікування - 0, дисперсія - 1. Математичне сподівання рівномірної складової постійно і прийнято рівним нулю.
>> sigma = 0: 0.1: 3 / 1,73;
>> n = 10;
>> for i = 1: length (sigma) x = normrnd (0,1, n, 1) + unifrnd (-1.73 * sigma (i), 1.73 * sigma (i), n, 1); [H, p1 (i), JBSTAT, CV] = jbtest (x); end;
>> n = 20;
>> for i = 1: length (sigma) x = normrnd (0,1, n, 1) + unifrnd (-1.73 * sigma (i), 1.73 * sigma (i), n, 1); [H, p2 (i), JBSTAT, CV] = jbtest (x); end;
>> n = 50;
>> for i = 1: length (sigma) x = normrnd (0,1, n, 1) + unifrnd (-1.73 * sigma (i), 1.73 * sigma (i), n, 1); [H, p3 (i), JBSTAT, CV] = jbtest (x); end;
>> plot (sigma, p1, 'or', sigma, p2, '+ b', sigma, p3, '. G')
>> grid on
Вид розподілу вибіркової статистики хі-квадрат. Розподіл генеральної сукупності формується як композиція нормального і рівномірного законів. Обсяг вибірки дорівнює 20 елементам. Кількість вибірок дорівнює 25. Графічна оцінка відповідності нормальному закону вибіркової статистики виконується за допомогою функції> qqplot.
>> m_norm = 0;
>> sigma_norm = 1;
>> m_unif = 0;
>> sigma_unif = 3 / 1,73;
>> n = 20;
>> N = 25;
>> for i = 1: N x = normrnd (m_norm, m_norm, n, 1) + unifrnd (m_unif-1.73 * sigma_unif, m_unif + 1.73 * sigma_unif, n, 1); [H, P, JBSTAT (i), CV] = jbtest (x); end;
>> qqplot (JBSTAT)
>> grid on