У трикутнику між його сторонами і кутами існують певні співвідношення. Якщо який-небудь кут трикутника більше іншого, то навпаки його лежить сторона з більшою довжиною, ніж навпаки іншого. Іншими словами, навпаки найбільшого кута трикутника лежить найбільша сторона, навпаки середнього кута - середня сторона, а навпаки самого маленького кута - найменша сторона.
Зрозуміло, що якщо кути трикутника рівні, то і сторони, навпроти яких вони лежать, рівні.
Сформулювати теорему про співвідношення сторін і кутів трикутника можна так: в трикутнику навпаки більшого кута лежить більша сторона. Однак можна сформулювати зворотну їй: в трикутнику навпаки більшої сторони лежить більший кут.
У прямій теоремі нам відомі розміри кутів, і з цього робиться твердження про розмір сторін. А в зворотної теоремі відомі розміри сторін, і робиться висновок про розміри кутів. Це означає, що при доведенні прямої теореми нам дано співвідношення кутів і потрібно довести співвідношення сторін. При доказі зворотного - дано співвідношення сторін, потрібно довести співвідношення кутів.
Доведемо пряму теорему. Нехай дано, що в ΔABC кут A менше кута B (∠A <∠B, или ∠BAC <∠ABC). Требуется доказать, что сторона, лежащая напротив ∠A, меньше, чем сторона, лежащая напротив ∠B.
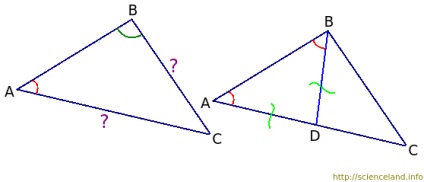
Навпаки ∠A лежить сторона BC, а навпаки ∠B лежить сторона AC. Потрібно довести, що BC Усередині ∠B від сторони AB відкладемо кут, рівний ∠A. Зрозуміло, що цей кут буде менше, ніж ∠B трикутника ABC, так як за умовою ∠A <∠B. Мы откладывали новый угол внутри ∠B, а значит полученная сторона нового угла пройдет внутри ∠B и пересечет сторону AC в некой точке. Назовем эту точку D. Таким образом, мы получили ∠ABD, который равен ∠A. Оскільки ∠A = ∠ABD, то ΔABD рівнобедрений. У нього сторона AD дорівнює стороні BD. Сторона AC складається з двох відрізків - AD і CD: AC = AD + CD. Але так як AD = BD ми можемо записати, що AC = BD + CD. Тепер розглянемо ΔBCD. У ньому BD і CD - це дві сторони. Третя сторона - це BC. Як відомо з теореми про нерівність трикутника, будь-яка його сторона менше суми двох інших. Тобто BC значить BC