Формула Хартлі не відображає випадково статистичного характеру подій, тому в загальному випадку необхідно забезпечити зв'язок між кількістю інформації і ймовірністю виникнення відповідних подій (повідомлень).
Це завдання вирішив в 1946 році американський математик Клод Шеннон.
При статистичному (ймовірному) підході інформація розглядається як міра ймовірності появи відповідного повідомлення.
З цієї точки зору, ніж подія більш імовірно, тим менше кількість інформації в повідомленні про нього ми маємо.
Багато видів повідомлень можуть бути зведені до подвійних подій.
У загальному випадку, подію можна розглядати результати результату деякого експерименту. Повна група за всіма можливими результатами вирішення даних ситуацій, називається ансамблем подій.
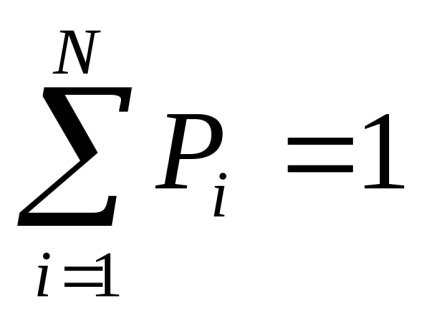
Нехай загальне число всіх можливих результатів одно N, з яких До не повторюються.
Тоді ймовірність якогось i-тієї події.
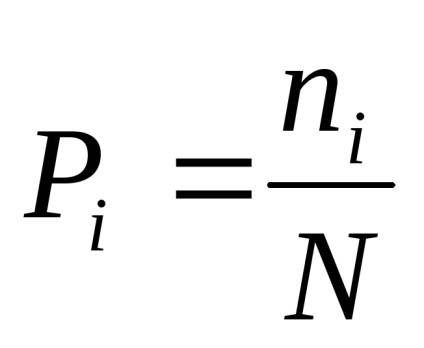
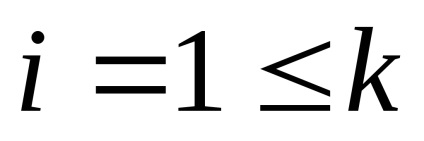
Кожна реалізація цієї події несе деяку кількість інформації

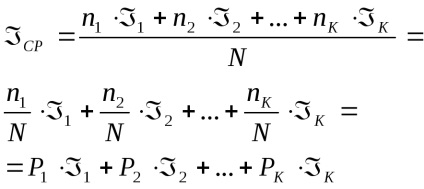
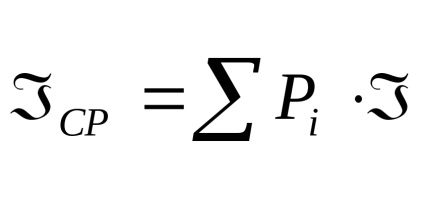
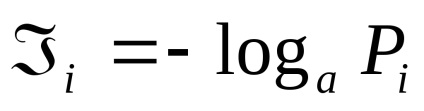
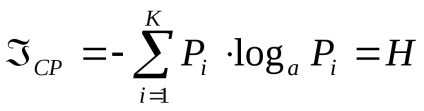
4 Статична міра інформації. Імовірність і інформація
Формула Хартлі не відображає випадково статистичного характеру подій, тому в загальному випадку необхідно забезпечити зв'язок між кількістю інформації і ймовірністю виникнення відповідних подій (повідомлень).
Це завдання вирішив в 1946 році американський математик Клод Шеннон.
При статистичному (ймовірному) підході інформація розглядається як міра ймовірності появи відповідного повідомлення.
З цієї точки зору, ніж подія більш імовірно, тим менше кількість інформації в повідомленні про нього ми маємо.
Багато видів повідомлень можуть бути зведені до подвійних подій.
У загальному випадку, подію можна розглядати результати результату деякого експерименту. Повна група за всіма можливими результатами вирішення даних ситуацій, називається ансамблем подій.
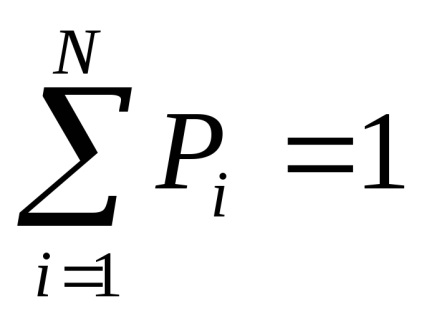
Нехай загальне число всіх можливих результатів одно N, з яких До не повторюються.
Тоді ймовірність якогось i-тієї події.
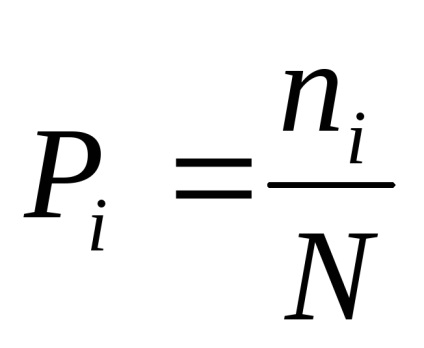
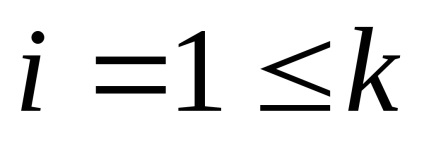
Кожна реалізація цієї події несе деяку кількість інформації

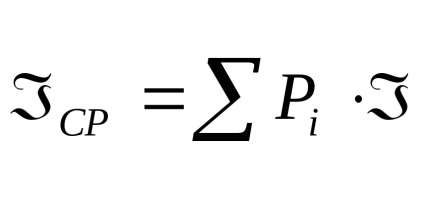
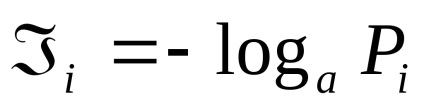
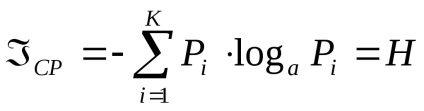
властивості ентропія
1. Ентропія вимірюється в тих же одиницях, що і кількість інформації.
Знак "-" у формулі (2) означає, що ентропія завжди нейтрально, тобто
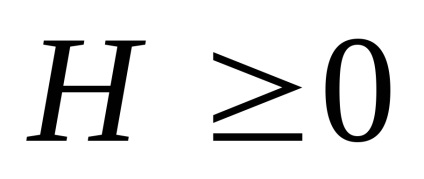
2. Ентропія М досягає максимуму, якщо всі події рівноймовірно.
3. Н = 0, якщо ймовірність однієї з i-тих подій дорівнює 1.
Таким чином, ентропія є мірою невизначеності в поведінці джерела повідомлень і характеризує здатність цього джерела видавати інформацію.
При збільшенні числа можливих станів системи енергія збільшується.
У загальному випадку, можна вважати, що кількість інформації характеризує зменшення ентропії в результаті процесу пізнання.
Якщо невизначеність знімається повністю, то кількість енергії дорівнює кількості інформації, виданої джерелом.
У разі неповного вирішення ситуації, кількість інформації визначається різницею між початковим і кінцевим значенням ентропії:
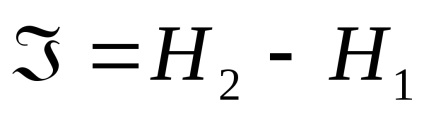
тобто кількість інформації буде визначатися різницею між початковим і кінцевим значенням ентропії.
Найбільша кількість інформації виходить, коли невизначеність знімається повністю.
Реальні події, а також символи в реальних співвідношеннях не є взаємно незалежними і рівноімовірними, яке реально переносить кожен окремий символ, буде менше максимально теоретично можливого значення.
Втрати кількості інформації характеризується коефіцієнтом надмірності:
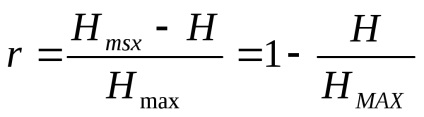
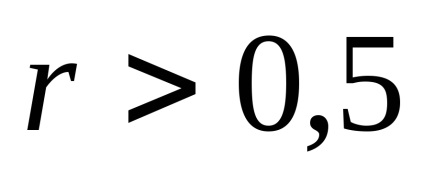
Для каналів передачі інформації використовують характеристику, звану швидкістю передачі інформації по каналах, вона дорівнює середній кількості інформації, яка може бути передана по каналу зв'язку в одиницю часу.
Середня кількість інформації, що видається джерелом повідомлення в одиницю часу, називається продуктивністю джерела.
Максимальна швидкість передачі інформації по каналу, називається пропускною спроможністю каналу.
Проблема узгодження продуктивності джерел сигналу і пропускної здатності передавального каналу, є однією з найважливіших задач теорії і практики кодування інформації.