Статечні функції, область визначення.
Хлопці, на минулому уроці ми дізналися, як працювати з числами з раціональним показником ступеня. На цьому уроці ми розглянемо статечні функції і обмежимося випадком, коли показник ступеня раціональний.
Ми будемо розглядати функції виду: $ y = x ^> $.
Розглянемо спочатку функції, у яких показник ступеня $ \ frac> 1 $.
Нехай нам дана конкретна функція $ y = x ^ 2 * 5 $.
Згідно з визначенням, яке ми дали на попередньому уроці: якщо $ x≥0 $, тобто область визначення нашої функції - це промінь $ [0; + ∞) $.
Таблиця значень.
Перейдемо до випадку, коли показник ступеня - правильна дріб (тобто, коли чисельник менше знаменника).
Давайте, порівняємо три статечних функції: $ y = x ^ 2 $; $ Y = x ^ $; $ Y = x ^ 3 $.
Число 2,5 лежить між 2 і 3, тоді здається, що і графік нашої функції буде лежати між відповідними графіками. Порівняємо значення функцій при різних х.
1. Якщо $ 0
На першому малюнку побудуємо графіки для випадку $ 0Властивості статечних функцій
Властивості функції $ y = x ^> $, $ (m> n) $:
1. $ D (y) = [0; + ∞) $.
2. Не є ні парною, ні непарною.
3. Зростає на $ [0; + ∞) $.
4. Не обмежена зверху, обмежена знизу.
5. Найбільшого значення немає, найменше значення дорівнює нулю.
6. безперервного.
7. $ E (f) = [0; + ∞) $.
8. опуклі вниз.
Графік функції $ y = x ^> $, $ (m> n) $ схожий на графік функції $ y = \ sqrt [n] $. Давайте схематично зобразимо наш графік функції. 
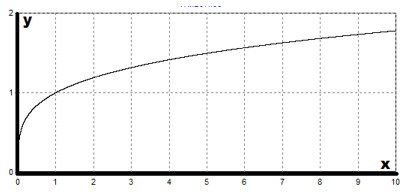
Властивості функції $ y = x ^> $, $ 0 0 $ і r - будь раціональне число, то похідна статечної функції $ y = x ^ r $ обчислюється за формулою: $ y '= r * x ^ $.
Приклад. Знайти найбільше і найменше значення функції $ y = x ^> $ на відрізку:
а) $ [1; 16] $,
б) $ (2,10) $,
в) на промені $ [9; + ∞) $.
Рішення.
Показник ступеня нашої функції позитивний. Тоді подивившись на властивості нашої функції ми бачимо, що вона зростає на всій області визначення. Це означає, що вона досягає свого найбільшого і найменшого значення на кінцях заданих відрізків (якщо вона визначена в цих точках).
а) $ y_ = 1 ^> = 1 $; $ Y_ = 16 ^> = (\ sqrt) ^ 5 = 4 ^ 5 = 1024 $.
б) Найбільшого і найменшого значення функції на цьому проміжку немає, так як нам дано відкритий проміжок, і точки 0 і 4 цього проміжку не належать.
в) Найбільшого значення немає.
$ Y_ = 9 ^> = \ sqrt = (\ sqrt) ^ 5 = 3 ^ 5 = 243 $.
Приклад. Знайти найбільше і найменше значення функції: $ y = \ fracx ^> - \ fracx ^ 4 $ на відрізку $ [1; 9] $.
Рішення.
Хлопці, ви пам'ятаєте як ми знаходили найбільше та найменше значення функції на відрізку в 10 класі?
Правильно, ми використовували похідну. Давайте вирішимо наш приклад і повторимо алгоритм пошуку найменшого і найбільшого значення.
1. Знайдемо похідну заданої функції:
$ Y '= \ frac * \ fracx ^> - x ^ 3 = 8x ^> - x ^ 3 = 8 \ sqrt-x ^ 3 $.
2. Похідна існує на всій області визначення вихідної функції, тоді критичних точок немає. Знайдемо стаціонарні точки:
$ Y '= 8 \ sqrt-x ^ 3 = 0 $.
$ 8 * \ sqrt = x ^ 3 $.
$ 64x ^ 3 = x ^ 6 $.
$ X ^ 6-64x ^ 3 = 0 $.
$ X ^ 3 (x ^ 3-64) = 0 $.
$ X_1 = 0 $ і $ x_2 = \ sqrt [3] = 4 $.
Заданого відрізку належить тільки одне рішення $ x_2 = 4 $.
Побудуємо таблицю значень нашої функції на кінцях відрізка і в точці екстремуму:
Відповідь: $ y _ = - 862,65 $ при $ x = 9 $; $ Y_ = 38,4 $ за $ x = 4 $.
Приклад. Вирішити рівняння: $ x ^> = 24-x $.
Рішення. Графік функції $ y = x ^> $ зростає, а графік функції $ у = 24-х $ убуває. Хлопці, ми з вами знаємо: якщо одна функція зростає, а інша убуває, то вони перетинаються тільки в одній точці, тобто у нас тільки одне рішення.
Зауважимо:
$ 8 ^> = \ sqrt [3] = (\ sqrt [3]) ^ 4 = 2 ^ 4 = 16 $.
$ 24-8 = 16 $.
Тобто при $ х = 8 $ ми отримали правильне рівність $ 16 = 16 $, це і є рішення нашого рівняння.
Відповідь: $ x = 8 $.
Приклад.
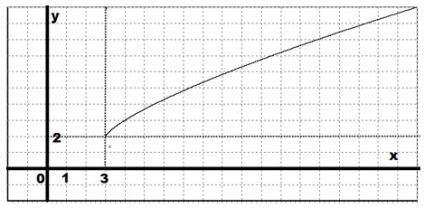
Побудувати графік функції: $ y = (x-3) ^ \ frac + 2 $.
Рішення.
Графік нашої функції виходить з графіка функції $ y = x ^> $, зміщенням його на 3 одиниці вправо і 2 одиниці вгору.
Приклад. Скласти рівняння дотичної до прямої $ y = x ^> $ в точці $ x = 1 $.
Рішення. Рівняння дотичної визначається відомою нам формулою:
$ Y = f (a) + f '(a) (x-a) $.
У нашому випадку $ a = 1 $.
$ F (a) = f (1) = 1 ^> = 1 $.
Знайдемо похідну:
$ Y '= - \ fracx ^> $.
обчислимо:
$ F '(a) = - \ frac * 1 ^> = - \ frac $.
Знайдемо рівняння дотичної:
$ Y = 1 \ frac (x-1) = - \ fracx + 1 \ frac $.
Відповідь: $ y = - \ fracx + 1 \ frac $.
Завдання для самостійного рішення
1. Знайти найбільше і найменше значення функції: $ y = x ^ \ frac $ на відрізку:
а) $ [1; 8] $.
б) $ (4,50) $.
в) на промені $ [27; + ∞) $.
2. Знайти найбільше і найменше значення функції $ y = \ fracx ^> - x $ на відрізку $ [1; 27] $.
3. Розв'язати рівняння: $ x ^> = 18-x $.
4. Побудувати графік функції: $ y = (x + 1) ^> - 1 $.
5. Скласти рівняння дотичної до прямої $ y = x ^> $ в точці $ x = 1 $.