Природа носіїв електричного струму в металах було встановлено в наступних експериментах.
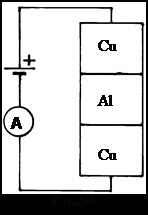
в. Досліди Річарда Толмена з співробітниками (Т.Стюард). 1916-1926 г, розвивали ідеї Мендельштамма Папалексі і дозволили отримати перші кількісні результати.
Котушка з великим числом витків розкручувалася навколо своєї осі, а потім різко гальмувалася. Кінці дроту котушки могли скручуватися і були приєднані до балістичному гальванометра. Магнітне поле землі ретельно компенсувалося провідниками з струмом. При різкому гальмуванні котушки гальванометр давав покидьок.
Якщо m - інертна маса носіїв електричного заряду, а e-их заряд, то гальмівний зміна імпульсу носіїв зарядів одно (mN) dv = Fdt = (eN) Edt (9.1)
Тут N число носіїв зарядів в обсязі проводу котушки.
Розділивши на N і взявши до уваги, що E = Uçl. де U - напруга на кінцях дроти, а l - його довжина, і що U = Ri; де R - опір ланцюга, а i - протікає в ланцюзі струм, отримуємо зміну імпульсу одиничного носія зарядів.
Проинтегрировав за часом гальмування котушки, отримуємо:
Лінійна швидкість обертання становила v = 300 м / с, довжина проводу котушки l = 500 м. Досліди з мідної, алюмінієвої, срібною дротами. При різних опорах ланцюга R і різних значень вимірюваних гальванометром заряду q питома заряд носіїв виявився однаковим і рівним eçm = 1,6 × 10 11 Кл / кг. Це було близько до результатів, отриманих Дж. Томсоном двадцятьма роками раніше в дослідах з катодними променями.
Узагальнення результатів перерахованих відповідей дозволило зробити наступні висновки:
Носії електричних зарядів у всіх металах однакові;
Носії електричних зарядів у металах цілком матеріальні, володіють інерцією і слабо пов'язані з кристалічною решіткою металу .:
Питома заряд носіїв становить eçm = 1,6 × 10 11 Кл / кг.
Оскільки до цього часу (кінець 20-х років XX століття) Міллікен визначив елементарний заряд e = 1.6 × 10 -19 Кл, то виявилося можливим оцінити інертну масу носіїв. .
Носіями струму в металах виявилися електрони, виявлені раніше в катодних променях (1897) і термоелектронів хмарі натрієвих металів. (1988, Т. Едісона).
В цілому електропровідність слід розглядати як явище переносу речовини і електричного заряду. Визначальним законом в останньому випадку є закон Ома.
2.Електронние теорія провідності металів. У першому десятилітті XX століття Пауль Друде і Гендрік Лоренц побудували класичну, тобто засновану на рівнянні Максвелла електронну теорію провідності металів.
Вони виходили з того, що валентні електрони в металах пов'язані зі своїми атомами настільки слабо, що можуть легко переміщатися від одного атома до іншого лише за рахунок енергії теплового руху. Така сукупність валентних електронів толковалась ними як електронний газ, що підкоряється статиці Максвелла Больцмана і є за своїми властивостями ідеальним.
Ідеальність електронного газу означає, що електрони провідності зіштовхуються між собою, вони соударяются лише з вузлами кристалічної решітки і знаходяться з ними в тепловій рівновазі. З цієї умови можна оцінити середню теплову швидкість електронів
Розглянемо, як пояснює теорія провідності Друде-Лоренца Закони Ома і Джоуля-Ленца. Для спрощення оцінок вважаємо, що всі електрони провідності мають однакову швидкість теплового руху - U.
а. Закон Ома . Якщо всередині металу створювати поле E. то на хаотичний рух електронів накладається рух, спрямований з деякою середньою швидкістю дрейфу v. Струм, поточний в провіднику перерізом S. дорівнює I = enSv. де n концентрація електронів провідності, e їх заряд. Щільність струму. (9.5)
Знайдемо середню швидкість дрейфу v. Будемо вважати, що електрон під дією сили eE в проміжок часу t від одного зіткнення з вузлом решітки до іншого рухається з прискоренням a і збільшує свою швидкість від 0 до. (9.6)
Оскільки рух електрона в електричному полі равноускоренное, то середня швидкість дорівнює половині максимальної; , (9.7)
а щільність електричного струму дорівнює. (9.8)
Формула (9.8) виражає закон Ома в диференціальній формі в електронній теорії. Коефіцієнт перед E розшифровує макроскопічну характеристику провідника, питому провідність g через сукупність мікрохарактерістік електронного газу.
Оцінимо середній час t вільного пробігу електронів провідності на прикладі міді. Вважаємо, що на кожен атом міді припадає один вільний електрон. Якщо M молярна маса міді, d її щільність, то концентрація вільних електронів. Підставивши n в вираз питомої провідності.
У проміжок часу t між двома зіткненнями електрон проходить середню відстань, що становить кілька десятків поперечних атомів.
Оцінимо середню швидкість дрейфу v електронів провідності в міді при напруженості поля E = 0,1 Вç м. З формули (9.7) отримуємо:
Швидкість дрейфу в мільярд разів менше теплової швидкості u = 10 5 м / с.
Зауважимо, що напруженість E = 0.1 В / м не такі вже й мала, як може здатися величина. Вона відповідає напрузі 0,1 В на кінцях дроти 1 м. При такій напрузі через мідний провід перетином S = 1 мм 2 проходить струм.
б. Закон Джоуля-Ленца. Маса електрона більш ніж в тисячу разів менше маси атомів у вузлах кристалічної решітки. Тому при неупругом зіткненні з вузлом електрон зупиняється, його швидкість звертається в 0, а його кінетична енергія дрейфу повністю віддається вузлу. Так як в момент зіткнення (формула 9.6), то енергія, що віддається електронами в одиниці об'єму протягом однієї секунда, дорівнює
Ця енергія виділяється у вигляді тепла, тому формула (9.9) виражає закон Джоуля Ленца в диференціальній формі. Вираз для питомої провідності (9.10)
вийшло те ж саме, що і в формулі закону Ома (9.8).
Строго кажучи, припущення, що електрон віддає всю енергію при зіткненні з атомом справедливо лише тоді, коли атом спочиває. Але атоми коливаються, а зіткнення не є абсолютно непружним. Тому електрони можуть як віддавати енергію (зіткнення з тікає атомом), так і отримати її (зіткнення з набігаючим атомом). У статистиці в умовах теплового рівноваги середня енергія руху електронів при постійній температурі залишається постійною.
Але коли електронний газ набуває спрямовану швидкість дрейфу, він набуває надлишкову над теплову енергію руху. Ця енергія електронів нерівноважна з енергією вузлів. Тому вона безперервно передається вузлів кристалічної решітки, підвищуючи температуру провідника.
в. Закон Видемана Франца. У 1853 році німці Г.Ведеман і Р.Франц встановили, що ставлення теплопровідності c до електропровідності g при одній і тій же температурі однаково у всіх металів. В 1882году датський фізик Людвік Лоренц показав, що це відно-шення пропорційно абсолютній температурі Закон Видемана-Франца. (9.11)
Тут L - коефіцієнт, однаковий для всіх металів, його називають числом Лоренца.
Класична електронна теорія так пояснює цей закон.
Оскільки електрони дуже рухливі, то можна вважати, що теплопровідність металів обумовлено в основному теплопровідністю його електронного газу. Його коефіцієнт теплопровідності дорівнює (9.12)
Тут l - середня довжина вільного пробігу електронів, u - їх середня швидкість теплового руху, i = 3 - число ступенів свободи електронів, k постійна Больцмана.
Підставивши в формулу (9.11) c з (9.12) і g з (9.10), де t = lçu. отримуємо: (9.13).
З кінетичної теорії ідеальних газів середня швидкість теплового руху електронів U 2 = 8kTçpm. Звідси (9.14).
Класична електронна теорія в цілому вірно тлумачить закон Видемана Франца. Вона розшифровує число Лоренца L = 8k 2 çpm як комбінацію констант і прогнозує лінійну залежність відносини cçg від температури T.
4. Труднощі класичної електронної теорії. Наведені вище висновки належать Друде і були зроблені їм в припущенні, що всі електрони провідності мають однакову швидкість u їх теплового руху.
Генрик Лоренц уточнив висновки, прийнявши Максвеловское розподіл електронів за швидкостями. В результаті у формулі закону Видемана Франца змінився коефіцієнт замість 8çp = 2,55 стало рівно 2. Однак уточнена формула стала гірше відповідати досвіду.
а.Молярная теплоємність металів повинна складатися з теплоємності вузлів решітки 3R і теплоємності ідеального газу електронів 3Rzç 2, де z число валентних електронів в атома. Повна теплоємність виходить рівної 3R + 3Rzç 2. Але досвід дає теплоємність 3R (Закон Дюлонга і Пті). Класична теорія не пояснює цього.
У формулі питомої провідності g = ne 2 l / 2mu величина середньої швидкості u відповідно до статистичної теорії ідеальних газів пропорційна кореню квадратному з температури. Так як, то u
. Звідси g = 1çr
. Але досвід дає лінійну залежність питомого опору від температури,, або r
T. Розбіжність нез'ясовно.
Зовсім не в змозі класична електронна теорія пояснити явище надпровідності. Суть його в тому, що при певній температурі, званої критичної Tк і близької до абсолютного нуля у більшості хімічно чистих металів, питомий опір провідника падає стрибком практично до нуля. Оцінимо, зроблені за часом загасання струму в надпровідний кільці, показує, що питомий опір надпровідників не більше 10 - 25 Ом × м. Для порівняння, питомий опір міді в звичайному стані дорівнює 1,7 × 10 -8 Ом × м.
У класичної електронної теорії r
, питомий опір має монотонно спадати з температурою, ніякого стрибка немає.
5. Межі застосування електронної теорії. Класична теорія електропровідності твердих тіл тим сильніше розходиться з експериментом, чим нижче температура провідника і чим вище концентрація електронів провідності. У тих випадках, коли температур досить висока, T> Tкомн. і концентрація носіїв мала, використання електронної теорії виправдано не тільки для якісних, а й для кількісних оцінок. Це дуже цінна можливість, оскільки класична електронна теорія Друде-Лоренца багато простіше і наочніше квантової електронної теорії.
Повернутися в зміст: