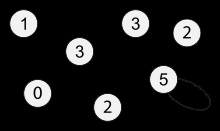
Мал. 1. Граф, на вершинах якого відзначені ступеня.
Ступінь вершини (англ. Degree. Також валентність. Англ. Valency) в теорії графів - кількість ребер графа G. інцідентних вершині x. При підрахунку ступеня ребро-петля враховується двічі. [1] Ступінь вершини позначається як d (x) (в західних джерелах - deg (v)). Максимальна і мінімальна ступінь вершин графа G позначаються відповідно Δ (G) і δ (G). На рис. 1 максимальний ступінь дорівнює 5, мінімальна - 0. В регулярному графі ступеня всіх вершин однакові, тому в даному випадку можна говорити про ступінь графа.
Лемма про рукостискання
За формулою суми ступенів для графа G = (V. E),
тобто сума ступенів вершин будь-якого графа дорівнює подвоєному числу його ребер. Крім того, з формули випливає, що в будь-якому графі число вершин непарної ступеня парне. Дане твердження (і сама формула) відомі як лема про рукостискання. Назва походить від відомої математичної задачі: необхідно довести, що в будь-якій групі число людей, потиснули руку непарному числу інших, парно.
Послідовність ступенів вершин

Мал. 2. Два неізоморфних графа з однаковою послідовністю ступенів (3, 2, 2, 2, 2, 1, 1, 1).
Послідовність ступенів вершин неорієнтованого графа є незростаюча послідовністю. [2] Для графа, зображеного на рис. 1, вона має вигляд (5, 3, 3, 2, 2, 1, 0). Послідовність ступенів вершин є інваріант графа. тому у ізоморфних графів вона однакова. Однак послідовність ступенів вершин не є унікальною ХАРАКТИРИСТИКИ графа: в деяких випадках неізоморфних графи також мають однакову послідовністю.
Проблема послідовності ступенів полягає в знаходженні деяких або всіх графів із заданою незростаюча послідовністю, що складається з натуральних чисел (нульові ступеня при цьому можуть бути проігноровані, так як їх кількість змінюється додаванням або видаленням ізольованих вершин). Послідовність, що є послідовністю ступенів будь-якого графа, називається графічної (англ. Graphical sequence). З формули суми ступенів слід, що будь-яка послідовність з непарної сумою (як, наприклад, 3, 3, 1) не може бути послідовністю ступенів графа. Зворотне також вірно: якщо послідовність має парну суму, вона являє собою послідовність ступенів мультиграфом. Побудова такого графа здійснюється досить простим способом: необхідно об'єднати вершини непарних ступенів в пари. до решти незаповненими вершин слід додати петлі.
Складніше реалізувати простий граф із заданою послідовністю. Теорема Ердеша - Галлай стверджує, що незростаюча послідовність di (при i = 1, ..., n) може бути послідовністю простого графа тільки якщо її сума парна і виконується нерівність
Наприклад, послідовність (3, 3, 3, 1) не може бути послідовністю простого графа; вона задовольняє нерівності Ердеша - Галлай тільки при k дорівнює 1, 2 або 4, але не при k рівному 3.
Згідно з критерієм Гавела-Хакимі [3]. якщо незростаюча послідовність (d1. d2. ..., dn) це послідовність ступенів простого графа, то (d2 - 1, d3 - 1, ..., dd1 +1 - 1, dd1 +2. dd1 +3. ..., dn) деяка послідовність ступенів простого графа. Цей факт дозволяє побудувати поліноміальний алгоритм знаходження простого графа із заданою реалізованої послідовністю.
Порівняємо вихідної послідовності чисел вершини графа без ребер з необхідними ступенями. Зазначене перетворення послідовностей задає як мінімум одну вершину графа, все інцідентние їй ребра і безліч вершин з новими необхідними доповненнями ступенів. Впорядковуючи решта вершини по незростання доповнень ступенів, отримаємо незростаюча послідовність ступенів простого графа. Повторюючи перетворення і впорядкування не більше n-1 разу, отримуємо весь граф.
Проблема знаходження або оцінки числа графів по заданій послідовності відноситься до області перерахування графів.
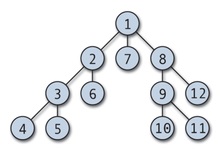
Мал. 3. кінцевими вершинами є 4, 5, 6, 7, 10, 11 і 12.
- Вершина ступеня 0 називається ізольованою.
- Вершина ступеня 1 називається кінцевий (англ. End vertex), висячої (англ. Pendant vertex) або листом графа (англ. Leaf vertex). Ребро, інцидентне такій вершині називається висячим (англ. Terminal (pendant) edge, end-edge). На рис. 3 висячим ребром є. Подібна термінологія використовується в вивченні дерев в загальному і як структур даних.
- Вершина ступеня n-1 графа порядку n називається домінуючою (англ. Dominating vertex).
- Якщо все вершини графа мають однаковий ступінь k. граф називають k -Регулярно або регулярним графом ступеня k. У цьому випадку сам граф має ступінь k.
- Ейлером шлях існує в неорієнтованому, зв'язкового графі тоді і тільки тоді, коли граф має 0 або 2 вершини непарної ступеня. Якщо граф містить 0 вершин непарної ступеня, Ейлеров шлях є циклом.
- Орграф є псевдолесом [невідомий термін] тільки якщо полустепені результату кожної вершини не більше 1. Функціональний граф - окремий випадок псевдолеса, в якому полустепені результату всіх вершин рівні 1.
- Згідно з теоремою Брукса, хроматичної число будь-якого графа за винятком кліки або непарного циклу не перевищує максимально його вершин (Δ). Згідно з теоремою Візінга, хроматичний індекс будь-якого графа не перевищує Δ + 1.
- k -вирожденним графом називається граф, в якому кожен підграф має вершину ступенем не більше k.