Тема дослідження
У яких сферах діяльності людини застосовується теорема Піфагора
Актуальність теми
В даний час загальне визнання отримало те, що успіх розвитку багатьох галузей науки і техніки залежить від розвитку різних напрямків математики.
Важливою умовою підвищення ефективності виробництва є широке впровадження математичних методів в техніку і народне господарство, що передбачає створення нових, ефективних методів якісного і кількісного дослідження, які дозволяють вирішувати завдання, що висуваються практикою.
Так чи актуальна теорема Піфагора зараз.
гіпотеза дослідження
Теорема Піфагора - це дуже важливе відкриття для людства. Чи так це?
цілі дослідження
Знайти з навколишнього середовища і вирішити завдання, які спираються на теорему Піфагора, торкнувшись такі області:
Результати дослідження
Діагональ d квадрата зі стороною а можна розглядати як гіпотенузу прямокутного рівнобедреного трикутника з катетом а. Таким чином, d = 2a, звідки: d = 2a2.
Діагональ d прямокутника зі сторонами а і b обчислюється подібно до того, як обчислюється гіпотенуза прямокутного трикутника з катетами a і b. Ми маємо d2 = a2 + b2
Висота h рівностороннього трикутника зі стороною а може розглядатися як катет прямокутного трикутника, гіпотенуза якого а, а інший катет a / 2. Таким чином маємо a = h + (a / 2), або h = (3/4) a. Звідси випливає h = 1/2 3a.
Куб, всередині якого проведена діагональ d, що є одночасно гипотенузой прямокутного трикутника. Катетами трикутника служать рабро куба і діагональ квадрата, що лежить в основі (як вказувалося раніше, довжина діагоналі дорівнює 2а). Звідси маємо d = a + (2a), d = 3a, d = 3a. Міркування, подібне до цього, можна провести і для прямокутного паралелепіпеда з ребрами a, b, з і отримати для діагоналі вираз d2 = a2 + b2 + c2
Досліджуємо піраміду, наприклад, таку, в основі якої лежить квадрат і висота якої проходить через центр цього квадрата (правильну піраміду). Нехай сторона квадрата - а, і висота піраміди - h. Знайдемо s (довжину бічних ребер піраміди). Ребра будуть гіпотенузи прямокутного трикутників, у яких один з катетів - висота h, а інший - половина діагоналі квадрата. (1/2 * 2a). Внаслідок цього маємо: s = h + (1/2) a. Потім можемо обчислити висоту h1 бічних граней. h1 = h + (1/4) a.
Вважати ці додатки теореми Піфагора тільки теоретичними - велика помилка. Якщо, наприклад, розглядати нашу чотирикутну піраміду як дах вежі, то в першому нашому питанні мова йде про те, якої довжини потрібно зробити бічні ребра, щоб при даній площі горища була витримана запропонована висота даху, а питання про величину бічної поверхні повинен цікавити, наприклад , покрівельника при підрахунку вартості покрівельних робіт.
У будівлях готичного і ромaнского стилю верхні частини вікон расчленяются кам'яними ребрами, які не тільки грають роль орнаменту, а й сприяють міцності вікон.
- У древніх (практичних) завданнях:
1.Над озером тихим,
2.Із підручника "Арифметика" на Русі.
3. Завдання індійського математика XII століття Бхаскару
В кінці дев'ятнадцятого століття висловлювалися різноманітні припущення про існування мешканців Марса подібних людині, це стало наслідком відкриттів італійського астронома Скіапареллі (відкрив на Марсі канали які довгий час вважалися штучними) і ін.
Природно, що питання про те, чи можна за допомогою світлових сигналів пояснюватися з цими гіпотетичними істотами, викликав жваву дискусію. Паризької академією наук була навіть встановлена премія в 100000 франків тому, хто перший встановить зв'язок з яким-небудь мешканцем іншого небесного тіла; ця премія все ще чекає щасливця.
Жартома, хоча і не зовсім безпідставно. було вирішено передати мешканцям Марса сигнал у вигляді теореми Піфагора.Неізвестно, як це зробити; але для всіх очевидно, що математичний факт, що виражається теоремою Піфагора має місце всюди і тому схожі на нас мешканці іншого світу повинні зрозуміти такий сигнал.
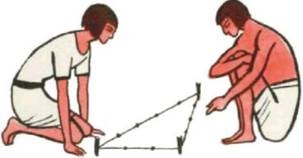
Єгипетський трикутник - прямокутний трикутник із співвідношенням сторін 3: 4: 5. Особливістю такого трикутника, відомої ще з часів античності, є те, що при такому ставленні сторін теорема Піфагора дає цілі квадрати як катетів, так і гіпотенузи, тобто 9:16:25. Єгипетський трикутник є найпростішим (і першим відомим) з героновой трикутників - трикутників з цілочисельними сторонами і площами. Назва трикутнику з таким відношенням сторін дали елліни: в VII - V століттях до н. е. грецькі філософи та громадські діячі активно відвідували Єгипет. Так, наприклад, Піфагор в 535 до н. е. за наполяганням Фалеса для вивчення астрономії і математики відправився в Єгипет - і, судячи з усього, саме спроба узагальнення відносини квадратів, характерного для єгипетського трикутника, на будь-які прямокутні трикутники і привела Піфагора до доведення знаменитої теореми. Єгипетський трикутник із співвідношенням сторін 3: 4: 5 активно застосовувався для побудови прямих кутів землемірами і архітекторами. (Завдання з вступної презентації) Для побудови прямого кута використовувався шнур або мотузка, розділена відмітками (вузлами) на 12 (3 + 4 + 5) частин : трикутник, побудований натягом такого шнура, з досить високою точністю опинявся прямокутним і самі шнури-катети були напрямними для кладки прямого кута споруди