Величина називається випадковою, якщо вона приймає свої значення в залежності від результатів деякого випробування (досвіду), причому для кожного елементарного результату вона має єдине значення. Випадкова величина називається дискретною. якщо безліч всіх можливих значень її звичайно.
Геометрично безліч всіх можливих значень дискретної СВ являє кінцеву систему точок числової осі.
Нехай Х - дискретна СВ. можливими і єдино можливими значеннями якої є числа х1. х2. ..., хп.
ймовірності цих значень (тобто pi є ймовірність події, що складається в тому, що Х приймає значення хi) /
Події Х = хі (i = 1, 2, ..., n), очевидно, утворюють повну групу подій, тому
Відповідність між усіма можливими значеннями дискретної СВ і їх можливостями називається законом розподілу даної СВ.
Для дискретної СВ закон розподілу зручно задавати таблицею
Перший рядок містить всі можливі значення СВ, а друга - їх ймовірності.
Випадкову величину Х будемо називати безперервної, якщо всі її можливі значення цілком заповнюють деякий кінцевий або нескінченний проміжок 
Для характеристики СВ Х вводять функцію розподілу
якщо число значень, які приймає функція розподілу лічильно, то Х - дискретна СВ, якщо нескінченно - безперервна СВ.
Властивості функції розподілу:
4) якщо x1
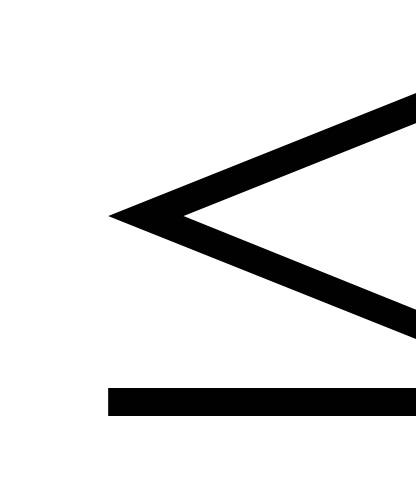
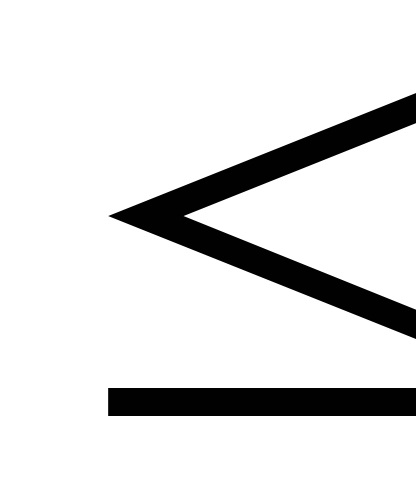
5) P (x1
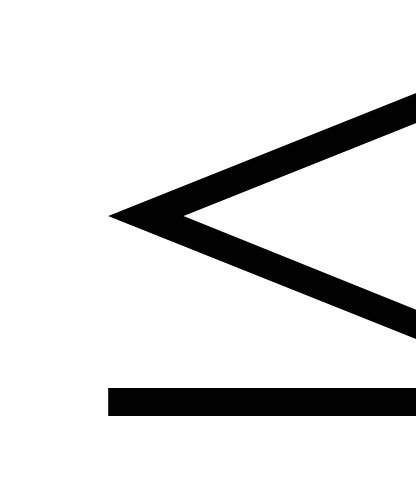
Припустимо, що для безперервної СВ Х її функція розподілу Ф (х) має безперервну похідну
f (x) називають щільністю ймовірності (для даного розподілу) або диференціальним законом розподілу СВ Х.
Послідовності псевдовипадкових чисел
Випадкові і псевдовипадкові числа, числа, які можуть розглядатися в якості реалізації деякої випадкової величини. Як правило, маються на увазі реалізації випадкової величини, рівномірно розподіленої на проміжку (0,1), або наближення до таких реалізацій, що мають кінцеве число цифр у своєму поданні. При такій вузькій трактуванні випадкове число (с. Ч.) Можна визначити як число, складене з випадкових чисел (с. Ц.). С. ц. в р -ічной системі числення є результатом експерименту з р рівноімовірними наслідками (кожному з результатів відповідає одна з р цифр). Експерименти з отримання кожної с. ц. передбачаються незалежними.
Джерелом с. ц. спочатку служили результати перепису населення та ін. таблиці чисел, отриманих експериментальним шляхом. Перші таблиці с. ц. були складені в 1927 у зв'язку з потребами математичної статистики (необхідністю випадкового вибору при плануванні експерименту). Надалі в зв'язку з виникненням методу статистичних випробувань були створені спеціальні експериментальні пристрої - датчики або генератори с. ч. засновані в більшості випадків на використанні шумів радіоелектронних приладів.
З розвитком методу статистичних випробувань також пов'язано виникнення поняття псевдовипадкових чисел (п. Ч.). Останні можна отримати шляхом обчислень за деякою заданою формулою (алгоритму), але їх властивості повинні бути близькі до властивостей с. ч. Найбільш поширені алгоритми, в яких кожне наступне число обчислюється за попереднім. Отримувані таким чином послідовності п. Ч. Мають період, що істотно відрізняє їх від послідовностей с. ч. Алгоритми отримання п. ч. ще недостатньо досліджені, але при обчисленнях за методом статистичних випробувань віддається перевага п. ч. т. к. властивості послідовності п. ч. можна досліджувати шляхом пробних обчислень, а експериментальні пристрої дають нові послідовності с. ч. при кожному їх використанні.
Випадкової називається величина із заданого діапазону, ймовірність появи якої визначається функцією закону розподілу. Приклад: рівномірний розподіл дискретної випадкової величини в діапазоні 1-6 - ймовірність дорівнює 1/6.
Отримання дійсно випадкового значення можливо тільки в тому випадку, якщо використовується фізичний або хімічний процес в якості задає механізму. За допомогою ЕОМ можна отримати псевдовипадкові послідовності. Для них характерно, що вибір однакових початкових значень призводить до генерації однакових послідовностей і існує таке N, чтоN + 1 член дорівнює першому члену послідовності.
У Сі присутні функції, що дозволяють генерувати послідовність псевдовипадкових цілих чисел, задавати початкове значення послідовності, задавати початкове значення випадковим чином (в залежності від системного часу).
Далі розглядаються методи генерації псевдовипадкових чисел.
6.1. Метод середніх квадратів
а) Вибирається довільне ціле 2k-значне чіслоx0. яке зводиться в квадрат, в результаті виходить 4k-значне число, з нього вибираються середні 2kзнака, які утворюють наступне випадкове число. Процедура повторюється необхідну кількість разів.
б) Беруться два довільних 2k-значних числа, які перемножуються і доповнюються до 4k-значности. З середини беруться 2kзнака, наступне число виходить з твору отриманого числа і попереднього.
Отримувані числа можна вважати псевдовипадковими, тому що середні знаки залежать від крайніх, які відкидаються.
6.2. мультиплікативний метод
Задаються константи Cіm. Береться довільне число, таким псевдовипадковим числом буде поточний, помножене наCі розділене по модулюm.
6.3. Адитивний метод (генератор Фібоначчі)
Визначається ціле число m. Беруться два цілих числа. Наступне число дорівнює сумі двох попередніх, взятої по модулюm.
6.4. лінійний метод
Визначається набором цілих чисел a [j], j [1, k] і целимm. Спочатку берутсяkцелих чисел. Наступне псевдовипадкове число дорівнює сумі поjот 1 доkпроізведенійa [j] xi + 1-j поділеній за модулюm.
6.5. комбінований метод
Береться ціле 2 k -значний чіслоx0. число
x0 'являє собою останні 2kразряда квадратаx0,
x0 '' - перші 2kразряда проізведеніяCx0 '(С - ціле число),
x0 '' '- перші 2kразряда квадратаx0' ',
x0 '' '' - останні 2kразряда квадратаx0 '' ',
Якість роботи генератора псевдослучайной послідовності можна визначити, побудувавши гістограму псевдовипадкових чисел, тому що закон розподілу рівномірний, то висота стовпців повинна бути приблизно однаковою.