Мал. 21. Виготовлення зубчастих коліс методом накатки
Останнім часом набуває поширення новий метод виготовлення коліс, званий методом накатки. Інструментом служить зубчасте інструментальне колесо. Нехай інструментальне колесо має z1 зубів модуля m. Потрібно з заготовки отримати зубчасте колесо з числом зубів z2 того ж модуля m. Для цього необхідно забезпечити відносний рух інструментального колеса і заготовки з передавальним відношенням
I1,2 = w2 / w1 = - z1 / z2, (7)
де w2 і w1 - кутові швидкості заготовки та інструментального колеса. Якщо матеріал заготовки досить еластичний, то інструментальне колесо видавить або, інакше кажучи, накатає на заготівлі необхідне число зубів модуля m (рис. 21). З точки зору кінематики можна одне з коліс зупинити, тоді друге буде обкатувати перше або обертати обидва колеса, але з кутовими швидкостями, що задовольняють умові (7). Накатка може відбуватися в холодному або нагрітому станах заготовки в залежності від пластичних властивостей її матеріалу. В даний час цим способом обробляють дрібномодульні зубчасті колеса. Перевагою цього методу є те, що одним і тим же інструментальним колесом можна накочувати колеса з будь-яким числом зубів загального модуля m. Для цього тільки має задовольнятися умова (7).
Вихідний виробляє контур евольвентного рейкового інструменту
Форма і розміри вихідного виробляє контуру (ІПК) стандартизовані. Евольвентні частини профілю зубів ІПК прямолінійні і нахилені до осі зуба під кутом a. Переходи від прямолінійної частини зуба до основи западини і до вершини здійснені по дузі радіусом ro. Точки сполучення відзначені на ІПК буквами А, С, D, Е. Прямолінійний частина СD є евольвентної, а округлення АС і DЕ - неевольвентной частиною контуру. Пряма, що розділяє зуб по висоті на дві рівні частини, називається ділильної. На ІПК відзначаються ще чотири лінії, паралельні делительной прямий і проходять з підстав западин зубів, на їхню вершин і через точки сполучення С і D. Відстані між цими прямими висловлюють розміри зуба вихідного виробляє контуру по висоті і вимірюються відповідно величинами ha = h * a і з = з * m, де h * - коефіцієнт висоти зуба, а з * - коефіцієнт радіального зазору. Відповідно до стандарту: h * a = 1,0; з * = 0,25. Прямі, що проходять через точки С і D, називаються прямими граничних точок.
Розмірами вздовж делительной прямий є крок, товщина зуба і ширина западини. Крок р вихідного виробляє контуру, який вимірюється по будь-якої прямої, паралельної делительной, є величина постійна, рівна pm, де m - стандартний модуль. Товщина зуба ІПК по ділильної прямий дорівнює ширині западини sо = ео = pm / 2, а разом вони складають крок. Кут профілю зуба стандартизований: a = 20 °. Радіус округлення (дуги DЕ)
ro = з * m / (1 - sina) = 0,4m. (8)
Таким чином, ІПК рейкового інструменту характеризується чотирма стандартними параметрами: m, a, h * a, с * (рис. 22).
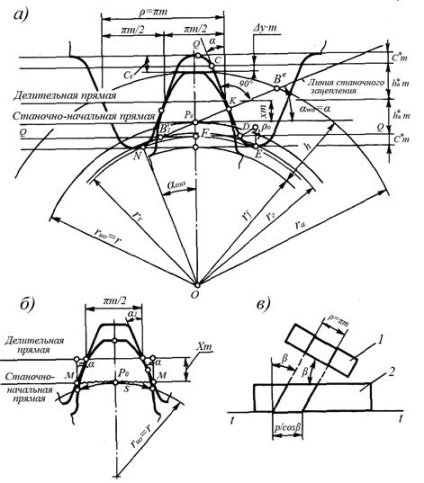
Мал. 22. Вихідний виробляє контур:
а) геометричні параметри рейкового зачеплення;
б) профіль зуба колеса; в) крок косозубого колеса
Рейкове верстатне зачеплення
Рейкове верстатне зачеплення, як і будь-яке зачеплення, має початкові лінії. Ними є верстатного-початкова пряма рейки і верстатного-початкова окружність колеса. Нагадаємо, що верстатного-початкові лінії котяться один по одному без ковзання. Можна показати, що в рейковому станочном зачепленні радіус rwo верстатного-початкового кола дорівнює радіусу ділильної окружності r.
Кут рейкового верстатного зачеплення awo дорівнює профільному кутку a вихідного виробляє контуру (як кути із взаємно перпендикулярними сторонами). Відзначимо також, що кут профілю зуба колеса в точці, що знаходиться на ділильної окружності, дорівнює профільному кутку a вихідного виробляє контуру.
На верстаті інструмент можна розташувати по-різному щодо нарізається колеса. Тому в станочном зачепленні делительная пряма ІПК може розташовуватися по-різному по відношенню до ділильної окружності колеса: 1) вона може стосуватися ділильної окружності - нульова установка інструменту; 2) бути відсунутою від неї - позитивна установка; 3) перетинати її - негативна установка.
Відстань між ділильної прямий і ділильної окружністю називається зміщенням інструменту. Його виражають у вигляді твору модуля m на коефіцієнт зміщення х і йому присвоюють знак. При нульовій установці зміщення mх = 0, x = 0. При позитивній установці mх> 0, х> 0. При негативній установці зміщенням є стрілка сегмента, яку делительная пряма відсікає від ділильної окружності; в цьому випадку mх <0, х <0.
На рис. 22 зображено рейкове верстатне зачеплення при нарізанні зубчастого колеса з позитивним зміщенням і вказані всі елементи виробляє вихідного контуру, який нарізається колеса і верстатного зачеплення.
Лінія рейкового верстатного зачеплення починається в точці N і через полюс Po йде в нескінченність. Довжина її активної частини обмежена точками B1 'і B' ', що знаходяться на перетині лінії верстатного зачеплення з прямою QQ граничних точок і окружністю вершин.
Профіль зуба колеса має евольвентної і неевольвентную частини. Перехід евольвентного профілю в неевольвентний знаходиться на колі граничних точок колеса, радіус якої r1 = ОВ1.
Відстань між окружністю вершин зубів колеса і прямий западин ІПК є верстатний зазор co. Величина його складається з двох частин: з * m і Dуm, де Dy - коефіцієнт зрівняльного зсуву.
4. ПОРЯДОК ГЕОМЕТРИЧНОГО РОЗРАХУНКУ евольвентної ПЕРЕДАЧІ
Товщина зуба евольвентного колеса по окружності довільного радіуса
Нехай дано зубчасте колесо, параметри якого становлять b, х, а, # 945 ;. Потрібно визначити товщину зуба по колу, радіус якої має довільну величину, але не меншу.
Підставивши ці вирази в вихідне рівняння, отримаємо:
Тут дуже важливо звернути увагу на те, що при збільшенні коефіцієнта зміщення х товщина зуба Sа буде зменшуватися внаслідок швидкого, прогресуючого зростання. При деякому критичному значенні хкріт настає загострення зуба:. Небезпека загострення особливо велика у коліс з малим числом зубів (менше 17). Для запобігання зламу вершини загостреного зуба коефіцієнт зміщення х обмежують верхнім значенням хmax так, щоб товщина зуба, підрахована за рівнянням (14), була не менше 0,2m.
Коефіцієнт зміщення і кут зачеплення евольвентної зубчастої передачі
З огляду на, що початкові окружності котяться один по одному без ковзання, запишемо
де і - товщина зубів, і - ширина западин за початковими колами коліс зубчастої передачі (рис. 23).
Так як початкові окружності перекочуються без ковзання, то кроки і рівні один одному:. Крок, або, оскільки,
Запишемо розгорнуті вираження величин,,, застосувавши до початкових кіл рівняння (13) і враховуючи, звичайно, рівняння:
Мал. 23. Зубчасте зачеплення
Підставивши ці вирази в рівняння (15) і виконавши нескладні перетворення, отримаємо
Після підрахунку за рівнянням (17) сам кут слід визначити за таблицями евольвентної функції.
Так як в загальному випадку, то, як випливає з рівняння (17),, т. Е.. Значить, в загальному випадку кут зачеплення.
Міжосьова відстань зубчастої передачі (див. Рис. 23)
Розрахунок евольвентної зубчастої передачі
Вихідними даними для розрахунку є параметри вихідного контуру інструмента, числа зубів коліс (z1 і z2) і коефіцієнта зсуву інструмента (x1 і x2).
До параметрів вихідного контуру інструмента відносяться:
a - кут профілю інструменту;
- коефіцієнт висоти зуба;
c * - коефіцієнт радіального зазору;
r - коефіцієнт радіуса заокруглення зуба.
Коефіцієнти зміщення знаходяться по блокуючого контуру з урахуванням якісних вимог до передачі.
Перейдемо до написання рівнянь, необхідних для проектування евольвентної зубчастої передачі. Ці рівняння складаються з умови, що зуби одного колеса входять у западини іншого колеса номінально щільно, без бокового зазору (див. Рис. 23).
З формули (17) визначаємо, а потім і сам кут визначаємо за таблицями евольвентної функції.
Міжосьова відстань розраховується за формулою (20).
Використавши рівняння (12), висловимо міжосьова відстань через радіуси і ділильних кіл:
Так як в загальному випадку, то.
Тож уявімо міжосьова відстань так:
Тут у - коефіцієнт сприйманого зсуву.
Вирішуючи спільно рівняння (20) і (21) щодо у, отримуємо
Якщо, то ділильні окружності коліс торкаються один одного. Така передача називається нульовою і виходить, коли, (передача без зміщення) або коли (равносмещенная передача). При (позитивна передача) ділильні окружності коліс відсунуті один від одного на відстань. Якщо (негативна передача), то ділильні окружності перетинають один одного.
Складемо розрахункову формулу для коефіцієнта зрівняльного зсуву. При визначенні номінальних розмірів передачі повинні бути виконані дві умови: 1) зуби коліс повинні зачіпатися один з одним без бокового зазору; 2) між колами вершин і западин зубчастих коліс повинен бути радіальний зазор, де згідно ГОСТ. Виконання першої умови забезпечується тим, що міжосьова відстань виражається через сприймається зміщення за рівнянням (21). Друга умова вимагає, щоб
(Або). Вирішуючи спільно рівняння (21) і (23), отримаємо. Після підстановки і простих перетворень в останній рівності отримуємо