Важливим прикладним додатком термодинаміки є теплові машини. Під тепловою машиною розуміють пристрій, що перетворює деяку частину отриманого кількості теплоти в механічну роботу. Механічна робота в теплових двигунах виробляється в процесі розширення деякого речовини, яке називається робочим тілом. Як робоче тіло зазвичай використовуються газоподібні речовини (пари бензину, повітря, водяна пара).
Теплові машини ділять на два класи: машини одноразової дії (ракета, гармата і т.п.) і циклічні машини (парові машини, двигуни внутрішнього згоряння).
Циклом називається процес, початок і кінець якого - збігаються. Прикладом циклічного процесу є процес, зображений на малюнку 13.3. Робота циклу складається з роботи самої системи (ділянка abc) і роботи над системою (ділянка cda).
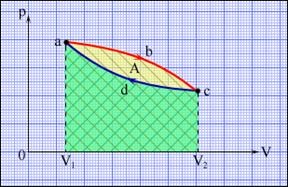
Малюнок 13.3 - Круговий процес на діаграмі (p. V). abc - крива розширення, cda - крива стиснення. Робота A в круговому процесі дорівнює площі фігури.
Робота циклу чисельно дорівнює площі фігури abcd. Газ виконує роботу на ділянці abc за рахунок отриманого від нагрівача кількості теплоти, а на ділянці cda над газом здійснюється робота зовнішніми силами. Щоб робота зовнішніх сил була менше роботи газу, необхідно її здійснювати при більш низькій температурі, а, отже, деяку кількість теплоти має перейти від робочого тіла - газу - до менш нагрітого тіла - холодильника. Енергетична схема теплової машини зображена на малюнку 13.4.
Твердження про те, що для здійснення корисної роботи в циклічному машині необхідна участь двох тіл з різною температурою, називається принципом Карно.
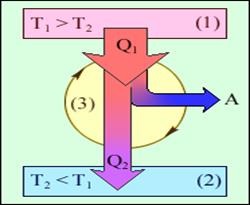
Малюнок 13.4- Енергетична схема теплової машини: 1 - нагрівач;
Цикл, за допомогою якого кількість теплоти, відібране від якого-небудь тіла, можна найкращим чином перетворити в механічну роботу, називається циклом Карно. Як робоче тіло тут виступає ідеальний газ. Цикл Карно складається з двох ізотерм і двох адіабати (рисунок 13.5).
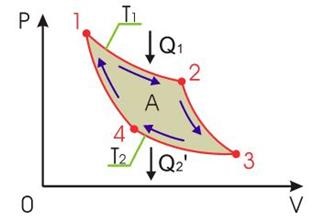
Малюнок 13.5- Схема циклу Карно
На ділянці 1-2 робоче тіло контактує з нагрівачем (тілом з великою теплоємністю) і отримує від нього кількість теплоти Q1. При цьому реалізується ізотермічний розширення газу (через великий теплоємності нагрівача його температура не змінюється). Це найвигідніший одноразовий процес, при якому все отримане кількість теплоти переходить в механічну роботу, згідно першому початку термодинаміки:
Ділянка 2-3 відповідає адіабатне розширенню ідеального газу. На цьому етапі розірваний контакт з нагрівачем і робоче тіло не обмінюється кількістю теплоти з іншими тілами. Це теж вигідно, оскільки в цьому випадку газ здійснює роботу за рахунок власної внутрішньої енергії, внаслідок чого вона зменшується, температура газу стає рівною Т2. Відповідно до першого початку термодинаміки,
На ділянці 3-4 робоче тіло приводиться в тепловий контакт з холодильником, що має більшу теплоємність і температуру Т2. Тут при більш низькій температурі газ стискають ізотермічні, здійснюючи над ним роботу, чисельно рівну відданому холодильника кількості теплоти, робота ж самого газу, так само, як і віддане кількість теплоти, негативна:
При більш низькій температурі, коли внутрішня енергія менше первісної, газ стискати легше, тому робота А34 менше роботи А12. Ізотермічне стиснення знову-таки є найвигіднішим, оскільки не потрібно змінювати внутрішню енергію газу, витрачаючи на це додаткову роботу зовнішніх сил. На останній ділянці циклу Карно необхідно повернути газ в первісний стан найвигіднішим чином, тобто адіабатно стиснути його. При адіабатні стисненні немає теплового контакту робочого тіла з холодильником, а робота зовнішніх сил повністю йде на збільшення внутрішньої енергії газу:
Корисна робота за цикл дорівнює алгебраїчній сумі робіт кожної ділянки циклу Карно:. Порівняння формул (13.25) і (13.28) дозволяє зробити висновок, що робота газу на ділянці 2-3 по величині дорівнює роботі газу на ділянці 4-1, але протилежна за знаком, отже, алгебраїчна сума робіт на цих ділянках дорівнює нулю, а робота за цикл буде визначатися сумою робіт ділянок 1-2 і 3-4:
Для подальшого перетворення корисної роботи розглянемо рівняння адіабати на ділянках 2-3 і 4-1, записані через обсяг і температуру: і. Поділимо друге рівняння на перше і отримаємо: або. З огляду на це рівність, можна винести за дужки натуральний логарифм відносини обсягів у формулі (13.29) і отримати вираз для корисної роботи за цикл Карно:
Ефективність роботи теплових машин характеризують коефіцієнтом корисної дії. який визначається як відношення корисної роботи, виробленої за цикл, до кількості теплоти, отриманого від нагрівача за цикл:
Підставами в цю формулу корисну роботу, вироблену за цикл Карно, яка визначається за формулою (13.40), і кількість теплоти, отримана від нагрівача, що визначається за формулою (13.25), після перетворення отримаємо вираз для розрахунку коефіцієнта корисної дії (ККД) циклу Карно:
Ця формула придатна тільки для розрахунку ККД циклу Карно. ККД інших циклів розраховують, використовуючи загальну формулу (13.41). У разі, коли є кілька нагрівачів, можна розрахувати отримане кількість теплоти, підсумовуючи кількості теплоти від кожного нагрівача, по формулі: