1.2.1. Епюр Монжа або ортогональні проекції.
Суть методу ортогональні (прямокутних) проекцій полягає в тому, що оригінал ортогонально проектують на 2 або 3 взаємно-ортогональні площини проекцій, а потім поєднують їх з площиною креслення.
1.2.2. Двухпроекціонной ортогональний креслення точки
Побудуємо просторову модель, на якій зобразимо дві взаємно перпендикулярні площини П1 і П2. Лінія перетину площини П1 і площини П2 називається віссю проекцій і позначається П2 / П1. Ось проекцій збігається з віссю ОХ.
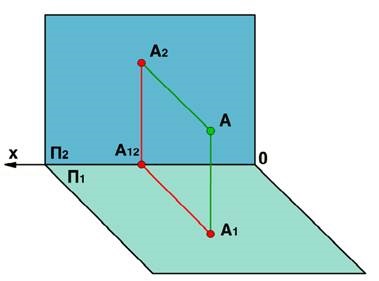
Виберемо в просторі точку А і опустимо з неї на площині П1 і П2 перпендикуляри. Тоді ми отримаємо дві проекції точки А: А1 - першу або горизонтальну проекцію точки А і А2 - другу або фронтальну проекцію точки А. Прямі А А1 і А А2 називаються проектується прямими або проектуються променями.
Перейдемо від моделі до креслення. Для цього подумки видалимо точку А і повернемо площину П1 разом з відрізком А1 А0 навколо осі проекцій П2 / П1 до суміщення з площиною П2.
Отриманий креслення називається епюр Монжа, ортогональним кресленням або комплексним кресленням.
Пряма А1 А0 співпаде з продовженням прямої А2 А0, і ми отримуємо пряму А1 А2, яка буде осі проекцій П2 / П1. Ця пряма називається лінією проекційної зв'язку або просто лінією зв'язку.
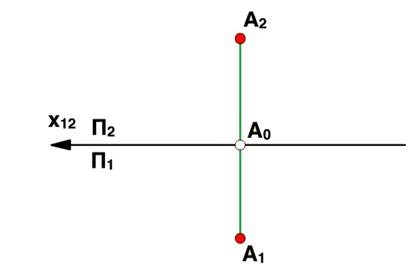
Лінія зв'язку - це пряма, що зв'язує пари проекцій однієї і тієї ж точки, і перпендикулярна осі проекцій.
У підсумку ми отримали двухпроекціонной комплексне креслення точки А.