Точки перегину графіка функції
Визначення. Точка графіка функції називається точкою перегину цього графіка, якщо існує така околиця точки осі абсцис, в межах якої графік функції праворуч і ліворуч від точки має різні напрямки опуклості.
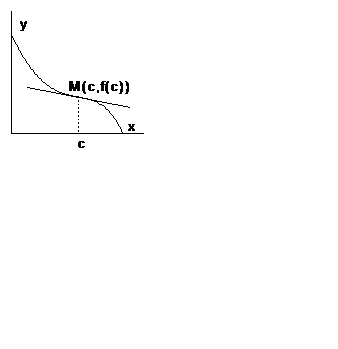
Якщо функція диференційована в точці і її околиці, то геометрично це означає, що графік функції переходить в околиці точки з одного боку дотичної на іншу (рис. 3).
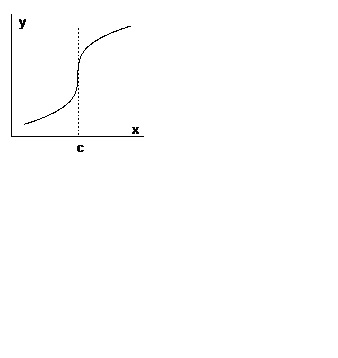
Якщо функція неперервна в точці. диференційована в околі точки. за винятком самої точки. і. то графік функції в околиці точки знаходиться по різні боки від вертикальної дотичній (рис. 4).
Теорема 3 (необхідна умова існування точки перегину). Нехай функція має в точці безперервну другу похідну. Тоді, якщо точка є точкою перегину графіка функції, то.
Зауважимо, що умова є необхідною, але недостатньою умовою перегину графіка функції в точці. Розглянемо, наприклад функцію. Друга похідна цієї функції. звертається в нуль точці. Однак на всій числовій осі. отже, всюди на цій осі графік функції має опуклість, спрямовану вниз, і точка не є точкою перегину.
Теорема 4 (достатня умова наявності точки перегину). Якщо функція диференційована в точці. двічі диференційовних в деякому околі точки. за винятком, можливо, самої точки і друга похідна змінює знак при переході аргументу через точку. то точка є точкою перегину графіка функції.
Зауважимо, що якщо функція неперервна в точці. двічі диференційовних в деякому околі точки. за винятком самої точки. і має в точці дотичну (хоча б паралельну осі), то твердження теореми 4 також справедливо.
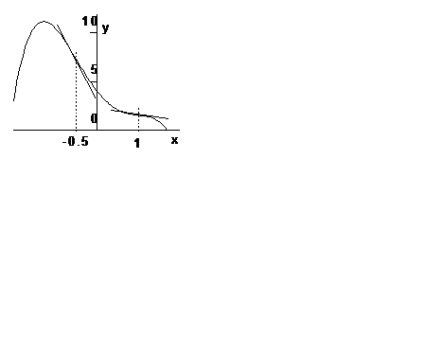
Приклад 1. Знайти точки перегину графіка функції.
Знайдемо похідні заданої функції:
,
.
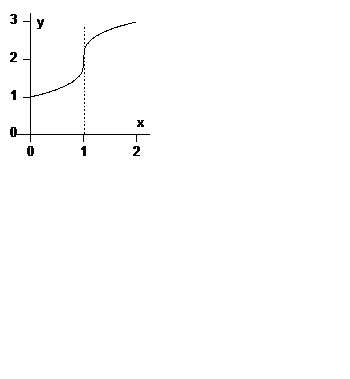
Приклад 2. Знайти точки перегину графіка функції.
Ця функція неперервна на всій числовій осі і має
Напрямок опуклості графіка функції
Нехай функція диференційована в будь-якій точці інтервалу. тобто має в будь-якій точці цього інтервалу кінцеву похідну. Тоді існує дотична до графіка функції. що проходить через будь-яку точку цього графіка. причому ця дотична не паралельна осі.
Визначення. Кажуть, що графік функції має на інтервалі опуклість, спрямовану вниз (вгору), якщо графік цієї функції лежить не нижче (не вище) будь-якої своєї дотичній.
На рис. 1 зображено графік функції, опуклою вниз, а на рис. 2 - опуклою вгору.
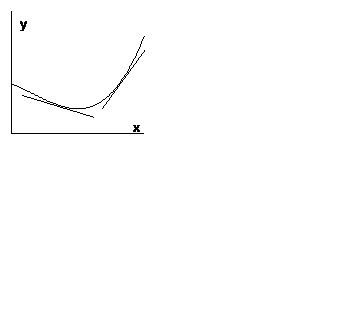
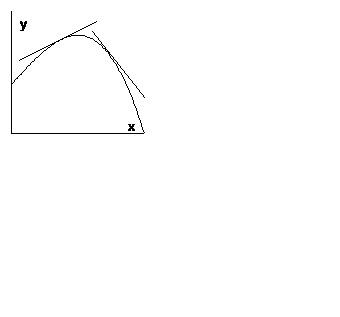
Теорема 1. Якщо функція має на інтервалі кінцеву другу похідну і якщо ця похідна неотрицательна (непозитивним) усюди на цьому інтервалі, то графік функції має на інтервалі опуклість, спрямовану вниз (вгору).
Теорема 2. Нехай друга похідна функції неперервна і позитивна (негативна) в точці. тоді існує така околиця точки. в межах якої графік функції має опуклість, спрямовану вниз (вгору).