У монографії представлені сучасні методи томографічної диаг-ностікі плазмових об'єктів за характеристиками світлової хвилі, випромінюваної або проходить через них. Викладаються математичні основи комп'ютерної Томо-графії, описані відповідні дво - і тривимірні алгоритми, що знайшли примі-ня в реальних експериментальних дослідженнях плазми. Дається коротка характеристика пакета прикладних програм ТО PAS, розробленого для завдань комп'ютерної томографії газу і плазми. Характеризуються конструктивні осо-сті плазмових томографічних систем, що працюють в емісійних, інтер - ферометріческіх і тіньових схемах збору діагностичної інформації. Прив-диться велика бібліографія за відповідними розділами теоретичних і експериментальних основ комп'ютерної томографії.
Книга призначена для фахівців в галузі фізики плазми, інфор-матики, обчислювальної математики, а також для студентів вузів відповідних спеціальностей.
Іл. 122. Бібліогр. 540 назв.
This monograph is devoted to the modern problem of plasma tomography diagnostics. It deals with interpretation of emission and transmission data in plasma experiments. Mathematical background of computerized tomography is given together with two- and three-dimensional algorithms that were applied in the real experimental investigations of plasma.
Software package "TOPAS" developed specially for gas and plasma tomography is described in short. The book presents characteristics of a wide variety of plasma tomography systems, that were developed for emission, interferometric and schlieren types of diagnostic setup.
The book is intended for academic and industrial researchers, especially those new to the field, and students.
РЕДАКЦІЙНА КОЛЕГІЯ СЕРІЇ
Е. П. Вовчків, Г.-Н. Б. Дандарон, Б. Н. Дев'яте (відп. Секр.), Г. А. Дюжев, М. Ф. Жуков (гл. Ред.), В. В. Кудінов, Ю. В. Курочкін, А. І. Леонтьєв, В. П. Лу-
кашов, О. Я. Новиков, А. А. Овсянников, І. Г. Паневіі, В. Д. Пархоменко, Л. С. Полак, Н. А. Рубцов, Л. М. Сорокін, П. І. Тамківі, Б. А. урюк (заст. гол. ред.), Ю. В. Цвєтков, BC Енгельшт
Рецензенти доктора фізико-математичних наук АЛ. Бухгейм, АН. ПАПИРІНА
Затверджено до друку Інститутом теоретичної та прикладної механіки СО РАН
Пропонована читачеві книга містить спробу розгляду завдань плазмової томографії, як вони бачаться з об'єднаних пози-цій експериментатора і теоретика.
Рішення обернених задач діагностики плазми було б неможливо без відповідного математичного апарату, тому описані також методи і алгоритми вирішення завдань плазмової томографії, від одновимірних до тривимірних, в межах фізичного рівня строгості.
ВСТУП В МЕТОДИ ТОМОГРАФІЇ
Останнім часом значний інтерес викликають процеси, що виникають при взаємодії потоків плазми між собою і з різного роду магнітними полями. Часто через складність такої взаємодії порушується осьова симетрія плазмового образо-вання. Тому при вивченні впливу зазначених полів на параметри плазми виникає необхідність використання томографічних ме-тодов дослідження.
У цьому розділі представлені основні принципи комп'ютерної томографії (КТ), а також особливості методів плазмової томографії (ПТ), що дозволяють визначати локальні параметри плазмових об'єктів при досить обмежених експериментальних даних.
1.1. ОПТИЧНІ МЕТОДИ
КТ - це область прикладної науки, що поєднує в собі досяг-ня обчислювальної математики, комп'ютерної техніки, фізики та багатьох інших сучасних наукових напрямків [485, 490, 534]. Розглянемо загальну постановку найбільш простий завдання емісійної і абсорбційної плазмової томографії в двовимірної випадку.
Рівняння переносу випромінювання уздовж прямої L має вигляд [514]
де е, х - відповідно локальні коефіцієнти емісії і аб-сорбції на фіксованій частоті v; I - координата вздовж прямої L, Рішення цього рівняння для виходить випромінювання запишеться так:
ФО) = J dle (l) exp [- / к (ОЛ '] • (1.1.2)
Інтегральне випромінювання плазми / "(£, р) (проекція) реєструється вздовж системи прямих променів (рис. 1.1), що задаються напрямком £ і відстанню р до початку координат 0 (іноді промені інтегрування задають в системі (р, в), де кут в характеризує кутове положення нормалі до променю; ми також іноді будемо використовувати нормальну систему завдання прямий).
Рис # 9632; 1.1. Томографическая регі-ція випромінювання плазми.
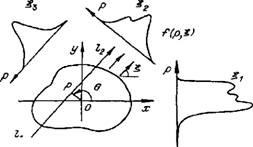
У наближенні опти-но тонкої плазми (я = 0) реєстроване випромінювання описується класичним інтеграли-ним перетворенням Ра-дона [457] (далі неіз-Укр локальні коеф-фициент емісії будемо
позначати через g (x, y), а реєстроване інтегральне випромінювання - через / Про ,!)):
На рис. 1.1 показано плоске перетин досліджуваного плазмового об'єкта з розподілом локальних коефіцієнтів емісії g (x, y). Вимірявши в діагностичних експериментах інтегральне випромінювання для набору кутів, £ £ (0,180 °), і набору координат, можна по-лучити оцінку шуканого рішення:g = R'a \ f + V) - (1.1.4)
Тут Л "1 - наближення до зворотного перетворення Радону; rj - шумова складова проекційних даних.
Методів поводження рівняння (1.1.3) в різних наближеннях присвячені наступні глави даної книги. Тут же схематично покажемо лише принципову можливість отримання такого рі-ня.
Введемо повернену на кут | систему координат (s, p): s = х cos | + У sin |, р = - xsinЈ + ycos |. (1.1.5)
У поверненою системі висловимо шукану функцію g (s, p) через її двовимірний Фур'є-образ g (vs, vp):
g (s, p) = ff Kv ^ exp + pvp)] dvsdvp. (1.1.6) - 00
Запишемо тепер вираз для проекції від функції g (s, p) в направ-лення s:
Др.1) = fg (s, p) ds = / / g (vs, v \ dv3dvj ds ехр [Дл (л> л + pv)] =
- / / Ехр [Oji (pvp) \ g (vslvp) 6 (vs) = advsdvp = - 00
= J Ayaplfljr ^ p ti (yt, v) I = 0. (1.1.7)
Легко бачити, що тут отримано вираз проекції через
зворотне фур'є-перетворення від фур'є-образу шуканої томограми g (vs, vp), взяте в центральному перерізі vs = 0. Звідси негайно слід так звана теорема про центральний перетині, що зв'язує між собою одновимірний Фур'є-образ проекції з двовимірним фурье - чином рішення:
Перепишемо рівняння (1.1.6) в полярній системі координат:
= F dЈ f g (v, Ј) exp [fbrvr sin (
Тут (r,
Тоді остаточно маємо формулу, відому як зворотне перетворень-тання Радону:
де р0 = - xsin | + Ycos | = Rsin (
Широко відомі успіхи медичної томографії, що дозволяє лікарю спостерігати на екрані дисплея структуру різних органів пацієнта, ставити діагноз його хвороби. У чому ж специфіка завдань плазмової томографії (ПТ), їх відмінність від завдань медичної КТ? Перерахуємо особливості завдань ПТ, що утрудняють їх рішення:
- трохи числа напрямків (ракурсів) спостережень К \
- трохи числа відліків (по р) N \
- кутові обмеження в реєстрації проекцій;
- можливе неузгодженість проекцій;
- наявність найрізноманітніших спотворюють сигнал апаратних функцій в системах детектування;
- наявність шумів з різною статистикою в вимірювальних ка-налах;
- поява в деяких випадках непрозорих включень внут-ри плазмових об'єктів;
- можливе відхилення променевих траєкторій від прямолінійних внаслідок рефракції.
Методи вимірювання проекційних даних в ПТ зазвичай є подальшим розвитком класичних способів отримання дл-ської інформації про плазму. В основному це емісійні (різного спектрального діапазону - від інфрачервоного до м'якого рентгенівського-го), трансмісійні: інтерферометричні (також в різних діапа-зонах електромагнітних хвиль), дефлектометріческіе (спекл-, шлірен- і тіньові), корпускулярні і т. П. Методи [422, 434, 501, 506, 507, 532]. Всі вони, звичайно ж, отримали свій розвиток перш за все для одноракурсних систем вимірювань. При відомих обмеженнях на клас досліджуваних плазмових утворень навіть такі системи збору даних можна віднести до томографічних, якщо вони дозволяють по виміряної інформації визначити локальні характеристики плазми в деяких її перетинах, а іноді і в повному обсязі.
До варіантів одноракурсних томографії відносяться завдання, в кото-яких відомі ізолінії (або ізоповерхні) локальних коеффіці-тів емісії. Найвідоміший приклад подібного роду - випадок осьової (або циліндричної) симетрії. Тоді ізолінії є концентричні кола, а єдина проекція / (р) пов'язана з шуканим рішенням g (r) інтегральним рівнянням Абеля:
рометріческой діагностики плазми на стелараторі JI-2 [370, 408], а також при діагностиці дугової плазми [442].
Слід підкреслити, що розвинена в [484] теорія реконструкції (заснована на більш ранній роботі [466]) дозволяє проводити одне - ракурсного томографірованія як в віяловій, так і в паралельній системі реєстрації. В роботі [260], орієнтованої на діагностику токамака ASDEX, отримані приватні результати для изолиний елліп-ної форми (співвісні ізолінії, а = р = 0 в (1.1.13)) при віялової схемою реєстрації.
Відомі плазмові установки, де розрахунки магнітних потоці »дозволяють припустити наявність трикутної системи ізоліній для локальних коефіцієнтів емісії. До їх числа відносяться торса трони, і, зокрема, для різних режимів роботи ТОРСАТРОНІ Ураган-3 [328] описані прості алгоритми інтерпретації одноракурсних віялових вимірювань для трьох видів систем изолиний [487, 489, 490]. Найбільш загальний випадок одноракурсних томографії описаний в [487, 489]. Тут інформація про вид изолиний шуканих коефіцієнтів емісії може бути задана у вигляді якоїсь іншої функції двох змінних В (х, у), найчастіше відомої в табличному вигляді [В ^. Прикладом таких функцій можуть служити розподілу магнітного потоку, що розраховуються в завданню про магнітне рівновазі.