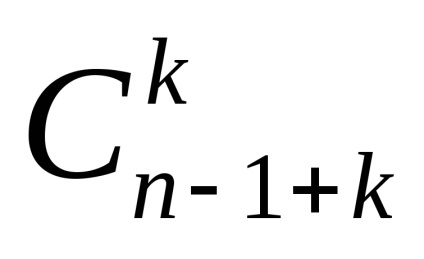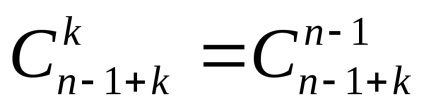Теорема 2. Загальна кількість вибірок в схемі вибораk елементів ізn без повернення і з урахуванням порядку визначається формулою
і називається числом розміщень ізnелементов поkелементов.
Доведення. Перший кулька можна вибратьn способами. При кожному з цих способів другий кульку можна вибратьn-1 способом, і т.д. Последнійk -й кульку можна вибрати (n-k + 1) способом. За теореме1. загальне число способів вибору одно
що й потрібно було довести.
Слідство 1. Число можливих перестановок безлічі ізn елементів естьn!
Д
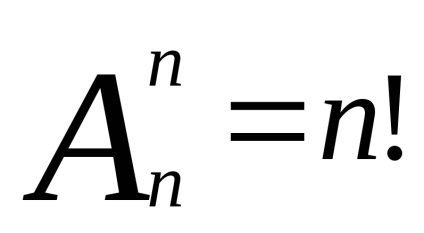
Урнов схема: вибір без повернення і без урахування порядку
Теорема 3. Загальна кількість вибірок в схемі вибораk елементів ізn без повернення і без урахування порядку визначається формулою
і
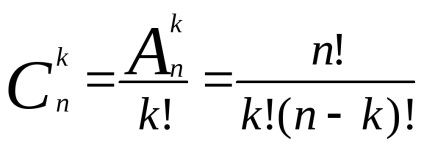
Доведення. Зауважимо, що, згідно з следствію1. з кожної вибірки даного складу (що складається ізk елементів) можна образоватьk! вибірок, що відрізняються один від одного тільки порядком елементів.
Тобто число вибірок, що розрізняються ще і порядком, в k! раз більше, ніж число вибірок, що розрізняються тільки складом. поділивши
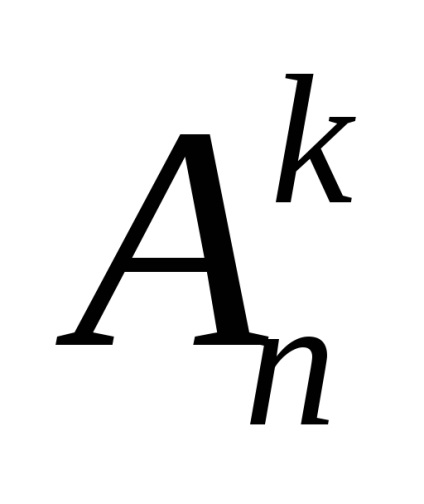
Урнов схема: вибір з поверненням і з урахуванням порядку
Т
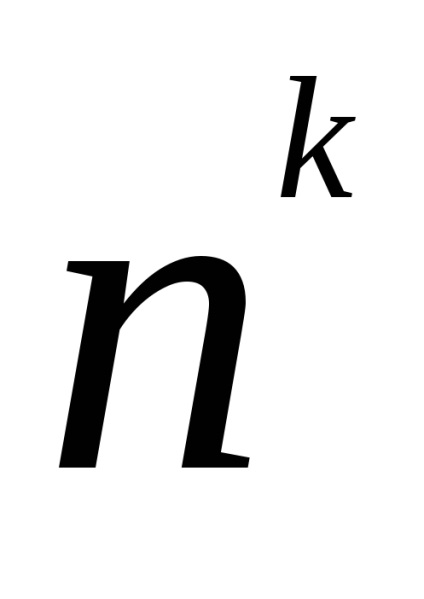
Доведення. Перший кулька можна вибратьn способами. При кожному з цих способів другий кульку можна вибрати такжеn способами, і такk раз.
Урнов схема: вибір з поверненням і без урахування порядку
Розглянемо урну з двома кульками і перерахуємо результати вибору двох кульок з цієї урни при виборі з поверненням:
З урахуванням порядку
Зауважимо, що в схемі «без урахування порядку» вийшло 3 різних результату на відміну від чотирьох в схемі «з урахуванням порядку». (Число 4 виникає і відповідно до теореми 4); і що ніяким розподілом на «число яких-небудь перестановок» число 3 з 4 отримати не вдасться.
Т
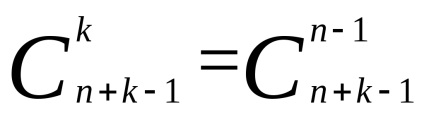
Доведення. Розглянемо докладно, чим відрізняються один від одного два різні результати такої схеми вибору. Нам не важливий порядок номерів, тобто ми враховуємо тільки, скільки разів в нашому наборі ізk номерів кульок з'явився кулька номер 1, кулька номер 2, .... кулька номерn. Тобто результат вибору можна уявити набором чіселk1, k2, ... kn. в которомki - число появ кульки номерi у вибірці, іk1 + k2 + ... + kn. = k. При цьому два результату експерименту різні, якщо відповідні їм набориk1, k2, ..., kn не збігаються.
Уявімо собі інший експеримент, який має точно такі ж результати (і, отже, їх стільки ж). Є n ящиків, в яких размещаетсяk кульок. Нас цікавить тільки кількість кульок в кожному ящику. Тобто, результатом експерименту знову є набір чіселk1, k2, ... kn. в которомki - число кульок в ящику з номеромi. іk1 + k2 + ... + kn. = k. Чіслаki як і раніше приймають натуральні значення або дорівнюють 0.
Атеперь зобразимо результат такого розміщення у вигляді схеми, в якій вертикальні лінії позначають перегородки між ящиками, а гуртки - знаходяться в ящиках кульки:
Ми бачимо результат розміщення 9 кульок по 7 ящиків. Тут 1-й ящик містить 3 кульки, 2-й і 6-й ящики порожні, 3-й ящик містить 1 кулька, і в 4-м і 5-м ящиках є по 2 кульки. Перекладемо одну кульку з першого ящика в другій і зобразимо таким же чином ще один результат розміщення:
Бачимо, що всі розміщення можна отримати, змінюючи між собою кульки і перегородки, або расставляяk кульок наn-1 + k місці. Чіслоn-1 + k виходить так: уn ящиків є ровноn + 1 перегородка, вважаючи крайні, іліn-1 перегородка, якщо не брати до уваги крайні, які рухати не можна. І естьk кульок. Перебравши всі можливі способи расставітьk кульок на етіхn-1 + k місцях (і ставлячи на місця, що залишилися перегородки), переберемо всі потрібні розміщення.
Але способів розставити k кульок наn-1 + k місцях рівно