УРОК №11. Рух небесних тіл. Приливні сили.
1. Обурена рух.
2. Завдання трьох тіл.
3. Теорія припливів.
4. Приливні сили в космонавтиці.
1. Обурена рух.
Фундаментальна задача небесної механіки - завдання n тіл полягає в наступному. У порожнечі знаходяться n матеріальних точок, що взаємодіють за законом всесвітнього тяжіння. Задані початкові положення і швидкості точок, необхідно визначити місце розташування будь-якого з цих тіл в будь-який момент часу. Для довільного n задача не вирішена досі. Хоча розвинені методи для чисельного вирішення цього завдання на комп'ютерах. Ці метоли дозволяють визначити місце розташування будь-якої точки із заданою точністю в будь-який кінцевий інтервал часу. Але ці методи не можуть відповісти на питання про поведінку точок на нескінченному інтервалі часу. А саме це питання є вкрай важливим для розуміння долі Сонячної системи, та й усієї світобудови.
Рішення завдання для n рівного один і два дано Ньютоном. Для n = 2 це рух по кеплеровским орбітах навколо загального центру мас. Такий рух, яке суперечить рішенню задачі двох тіл. називають необуреним. Насправді ж все тіла Сонячної системи притягуються не тільки Сонцем, а й один одним. Тому жодне тіло в Сонячній системі не може рухатися точно по еліпсу, параболі або гіперболі і тим більше по колу. Відхилення в рухах тіл від законів Кеплера називаються збуреннями, а реальний рух тіл - обуреним рухом. Обурення тіл Сонячної системи мають дуже складний характер, хоча вони і невеликі за величиною, так як сумарна маса всіх збурюючих тел в 700 разів менше маси Сонця.
ассмотрім на прикладі системи трьох тіл, як спрямована обурює сила. Нехай є три небесних тіла: Сонце З з масою М. планета Р1 з масою m1 на відстані r1 від центру Сонця і планета P2 з масою m2 на наполягання r2 від Сонця і на відстані r від планети P1. Всі три тіла діють один на одного за законом Ньютона. В інерціальній системі відліку, пов'язаної з центром мас, Сонце отримує прискорення у напрямку СР1 від планети Р1 і прискорення у напрямку СР2 від планети Р2. Перейдемо в неінерціальна геліоцентричну систему відліку, тобто розглянемо рух планети Р1 щодо Сонця. У цьому випадку на планету Р1 будуть діяти сили, що викликають такі прискорення: у напрямку РС1. у напрямку р1р2 і у напрямку паралельному Р2С.
Перше прискорення w є прискорення відносного руху, викликане тяжінням Сонця; воно відповідає за рух планети Р1 навколо Сонця (а не навколо загального центру мас) за законами Кеплера. Прискорення w 'і w "складають прискорення вимушених коливань і зумовлюють відхилення в русі планети Р1 від законів Кеплера. Отже, розглянутому випадку обурює сила складається з двох сил: з сили дії планети Р2 на планету Р1 і з сили дії планети Р2 на Сонце. Висновок: прискорення від возмущеніяwвесть різницю векторів прискорень, що викликаються возмущающим тілом на планеті і на Сонце. З малюнка видно, що в загальному випадку обурює сила не спрямована точно до обурює тіла Р2.
2. Завдання трьох тіл.
Точне рішення задачі руху небесних для випадку трьох тіл і більш в загальному вигляді, тобто вигляді кінцевих формул, що дозволяють точно розрахувати положення в просторі і швидкості всіх тіл в будь-який момент часу, в принципі неможливо. Загальне рішення для трьох тіл у вигляді нескінченних рядів знайдено в 1912 році, і то практично скористатися ним поки неможливо. В даний час завдання руху небесних тіл вирішуються чисельними м
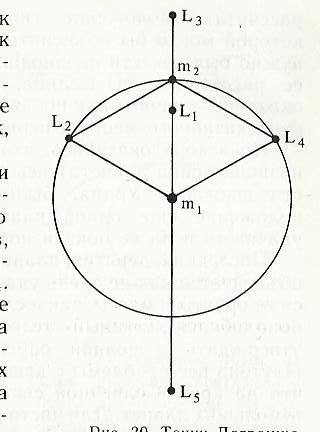
Одне з найцікавіших рішень завдання було знайдено Лагранжем для, так званої, обмеженою завдання трьох тіл. У ній розглядається рух системи трьох тіл, маси яких пов'язані співвідношенням: m1 >> m2 >> m3. В цьому випадку друге тіло рухається по кеплерова орбіті, а третє тіло знаходиться в одній з п'яти точок Лагранжа. Рух в точках L1. L3. L5 нестійке, а в точках L2 і L4 - стійке: третє тіло, потрапивши в одну з цих точок, буде знаходитися там постійно. У Сонячній системі існують подібні розташування небесних тіл, що виникли природним чином, наприклад, дві групи астероїдів, які рухаються по орбіті Юпітера в його точках Лагранжа L2 і L4. В майбутньому планується рукотворне використання точок Лагранжа в системі Земля - Місяць, в яких будуть розташовуватися ретрансляційні супутники для забезпечення постійного зв'язку між Землею і місячними станціями, розташованими на зворотному боці Місяця.
3. Теорія припливів.
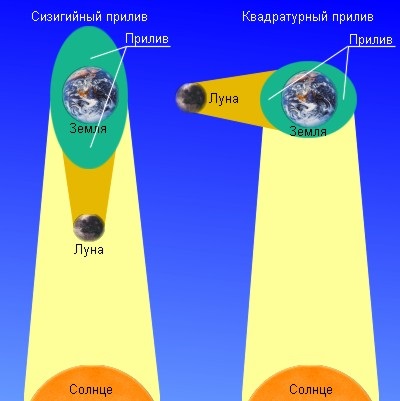
Двічі на добу в морях і океанах відбувається підйом і спад води. Уже в давнину спостерігачі помітили, що приплив настає через деякий час після кульмінації Місяця в місці спостереження. Більш того, припливи особливо сильні в дні ново-і повень, тобто коли центри Землі, Місяця і Сонця розташовуються приблизно на одній прямій. З огляду на це, Ньютон пояснив припливи дією сил тяжіння з боку Місяця і Сонця.
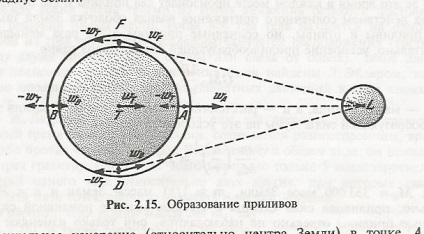
Запишемо вирази для прискорень, що створюються притяганням Місяця для різних точок Землі (притягання самої Землі поки не враховуємо). В інерціальній системі відліку, пов'язаної з центром мас системи Земля - Місяць, значення прискорень визначаються за формулами: де WА, wT, Wв - прискорення, викликані притяганням Місяця в точках А, T, В; М - маса Місяця; r - радіус Землі; R-відстань між центрами Землі і Місяця (R 60 r).

тсчета, необхідно з значень всіх прискорень відняти прискорення центру Землі.
Виконаємо дії в дужках і врахуємо, що r мало і їм можна знехтувати. Тоді В ідім, що приливні прискорення протилежні і спрямовані від центру Землі. Прискорення, що виникають в системі відліку, пов'язаної з тілом, через те, що внаслідок кінцевих розмірів цього тіла різні його частини по-різному притягуються возмущающим тілом, називаються приливними ускорениями іобратно пропорційні кубу расстояніядо обурює тіла, а відповідні їм сили називаютсяпрілівнимі силами.
У точках А і В прискорення вільного падіння g виявляється менше норми, а в точках F і D, в яких рівнодіюча сил спрямована майже до центру Землі більше. Тиск води в океані на однаковій відстані від центру Землі має бути однаковим. Тиск стовпа води визначається виразом P = gh. Ясно, що висота стовпа h повинна бути більше в тих місцях, де прискорення сили вільного падіння менше, тобто де менше вага стовпа води, і навпаки. Значить, в точках А і В вода підніметься вище середнього рівня, утворюючи так званий приливний горб, щоб зрівняти тиск, а в точках F і D буде нижче норми, в цих точках спостерігається явище відливу.
Насправді картина виходить ще більш складною, так як Земля обертається навколо своєї осі набагато швидше, ніж Місяць оббігає навколо неї, тому приливний горб рухається по поверхні Землі, залишаючись весь час навпроти Місяця. За час між двома послідовними кульмінаціями Місяця, що дорівнює в середньому 24 год 52 м. Приливні горби обійдуть навколо всієї земної кулі, і в кожному місці відбудеться за два припливи і два відливи.
П
Місяць викликає припливи не тільки в океанах, а й в корі Землі, і в атмосфері. Під впливом приливних сил літосфера витягується приблизно на півметра. Тертя води об дно, а також деформація твердої оболонки Землі супроводжується виділенням тепла, що призводить до зменшення механічної енергії системи Земля - Місяць, т. Е. До сповільнення обертання Землі. Кожне століття тривалість діб збільшується приблизно на 0,002 с. Два мільярди років тому тривалість земної доби становила всього 10 годин, а в далекому майбутньому вони будуть прирівнюються до одного місяця. Уже тепер завдяки приливні силам Місяць постійно обернений до Землі однією і тією ж стороною, т. Е. Коли Місяць обертався з іншою швидкістю, і наші пращури бачили зворотний бік Місяця, але так як Місяць значно менше Землі, вона зупинилася швидше. Крім того, тяжіння приливних виступів, які обганяють Місяць через більш швидкого обертання Землі, захоплює Місяць по орбіті вперед, в результаті чого вона віддаляється від Землі зі швидкістю близько 3 см в рік, переходячи на більш високу орбіту.
4. Приливні сили в космонавтиці
Рух штучних супутників Землі (ШСЗ) відбувається за законами небесної механіки, але не завжди його можна вважати матеріальною точкою, тому в окремих випадках слід враховувати дію приливних сил. Приливні прискорення в симетрично розташованих відносно центру ваги супутника точках, що знаходяться на одній лінії з центром Землі, протилежні за знаком і рівні: де а - модуль приливної прискорення; h - висота супутника над Землею; l -проекція відхилення даної точки від центра ваги ШСЗ на лінію центр Землі - центр ваги ШСЗ. Приливні прискорення завжди спрямовані від центру ваги ШСЗ, тобто всі речі, які ви залишили висіти в просторі супутника рано чи пізно опиняться у його бортів. Розрахуємо конкретний приклад. Нехай на відстані 3 м від центра ваги супутника знаходиться незакріплений предмет. Рух предмета під час вільного польоту супутника визначається тільки мікроускореніямі, створеними приливними силами. Підставами відомі дані (l = 3 м, g = 9,8 м / с 2. R = 6,378 * 10 6 м), отримаємо приливної прискорення всього 10 -5 м / с 2. Але навіть при такому малому прискоренні через десять хвилин предмет виявиться приблизно на 2 м ближче до корпусу супутника, ніж був. Перевіримо це. Відстань d. яке проходить тіло за час t. має прискорення а й нульову початкову швидкість дорівнює:. Тому домогтися в ШСЗ повної невагомості практично неможливо.
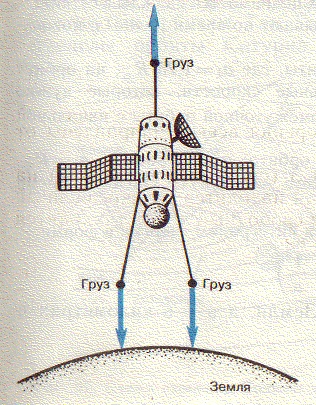
Але іноді приливні сили відіграють позитивну роль. Так, для багатьох ШСЗ необхідно зберігати певну орієнтацію відносно Землі. Наприклад, метеорологічні супутники ведуть безперервну зйомку хмарного покриву Землі. Природно, об'єктиви апаратури ШСЗ повинні бути завжди спрямовані на Землю. Як приливні сили Землі за мільярди років встановили Місяць однією стороною до Землі, точно так же вони розгортають і супутники потрібної стороною до Землі, тільки, звичайно, значно швидше. Робиться це в такий спосіб. На довгих і легких штангах кріпляться невеликі вантажі. Приливні сили, що діють на ці вантажі, будуть розгортати ШСЗ так, щоб штанги розташувалися уздовж радіуса Землі. Тим самим буде забезпечена необхідна орієнтація супутника.
1. Як будуть відрізнятися періоди обертання штучних супутників Землі і Місяця, якщо ці супутники знаходяться на однакових відстанях від їх центрів?
2. Обчисліть масу Марса в порівнянні з масою Землі по руху його супутника Фобоса, для якого а = 9300 км, Т = 0,32 сут.
3. Місяць в апогеї на 1/9 далі, ніж перигеї. На скільки відсотків в перигеї приливна сила більше, ніж в апогеї?
Питання експрес опитування.
1что більше: прискорення, що повідомляється Землею Сонця або повідомляється Землею Місяці?
2. Чому найбільші припливи бувають за часів повень і молодиків?
3. Чому в штучному супутнику Землі не можна досягти невагомості?
4. Як змінюється рух Землі під дією приливних сил?
5. Як спрямовані приливні сили по відношенню до центру Землі?
6. На які фази Місяця припадають найменші припливи на Землі?
7. Що таке невозмущенное рух?
8. Чому припливи і відливи тривають не по 12год, а по 12год. 26мін.?
9. Яку характеристику небесних тіл дозволяє обчислити 3-й закон Кеплера?
10. Чому Місяць завжди звернена до Землі однією стороною?
11. Чому стабілізуючі вантажі на ШСЗ виносять назовні на довгих штангах?