Після цього можна викликати процедуру інтерполяції, вказавши описані вище списки її параметрами і, крім того, прийнявши х за змінну інтерполяції.
Варто зауважити, що в якості результату процедурою interp () повертається вираз, а не оператор, як це було вище при розробці процедури побудови інтерполяційного полінома Лагранжа.
Ще один досить популярний спосіб інтерполяції полягає в наступному. На кожному інтервалі між сусідніми вузловими точками інтерпольованої функції представляється у вигляді полінома. Але на відміну від, скажімо, інтерполяції Лагранжа, де один і той же поліном використовується для всіх точок, в даному випадку на кожному інтервалі поліном свій. Крім рівності інтерполяційної функції у вузлах табличних значень функції інтерпольованої, на першу накладається ще й умова безперервності похідних до порядку, на одиницю меншого, ніж ступінь інтерполяційних поліномів. Подібний тип інтерполяції називається інтерполяцією сплайнами, або сплайн-інтерполяції. Найбільшою популярністю користується інтерполяція кубічними сплайнами.
У Maple для виконання інтерполяції сплайнами може бути використана процедура spline (). Процедура має три обов'язкових параметра. Перші два - це списки з вузловими точками і значеннями функції відповідно. Третім параметром вказується змінна інтерполяції. Якщо четвертий необов'язковий параметр не вказано, то інтерполяція виконуватиметься кубічними сплайнами, тобто для "зшивання" вузлових точок будуть використовуватися поліноми третього ступеня. Наприклад, якщо параметрами процедури вказати раніше розглянуті списки, табулірует значення функції у вузлових точках, отримаємо такий результат.

Четвертим параметром процедури spline () може бути або одне із зарезервованих ключових слів з набору linear (інтерполяція лінійними залежностями), quadratic (інтерполяція параболами), cubic (кубічний сплайн), quartic (інтерполяція поліномами четвертого ступеня), або ціле невід'ємне число, яке визначає ступінь інтерполяційного полінома. Причому вказівку числа від 1 до 4 еквівалентно використанню перерахованих текстових опцій, згідно того порядку, як вони були представлені вище.
Увага!
В якості четвертого параметра може бути зазначено будь-яке ціле позитивне число, не тільки в діапазоні від 1 до 4. Просто для цих чисел існує альтернативний виклик через текстову опцію. Наприклад, командою spline (X, У, х, 5) можна виконати інтерполяцію розглянутої вище функції поліномами п'ятого ступеня і т.д.
Інтерполяція поліномами четвертого ступеня все тієї ж функції виглядає наступним чином.

Вирази досить громіздкі. Подивимося, що буде, якщо використовувати в якості сплайн-полиномов лінійні залежності.

У порівнянні з попереднім випадком, тут отриманий простіший результат. Однак простота - далеко не завжди означає ефективність. У цьому неважко переконатися, якщо побудувати графіки для інтерполяційних функцій, одержуваних при сплайн-інтерполяції поліномами різних ступенів.
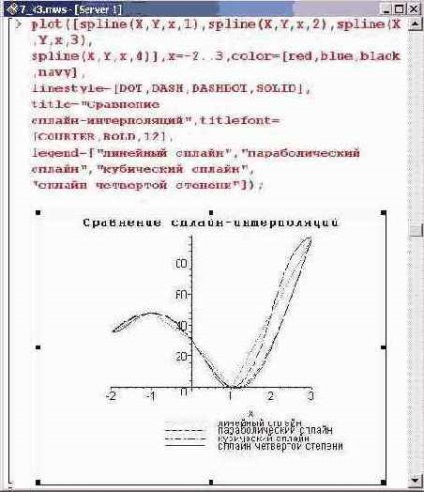
Очевидно, що лінійна сплайн-інтерполяція є досить грубою. За великим рахунком, це просто з'єднання інтерполяційних крапок лініями. Такий тип інтерполяції використовується вкрай рідко. Що стосується використання поліномів інших ступенів, починаючи з другої, то візуально особливої різниці між ними (у всякому разі в даному прикладі) немає. Однак не слід забувати, що ступінь сплайн-полиномов визначає гладкість отриманих кривих. Це важливо особливо в тих випадках, коли від отриманих в результаті інтерполяції функцій слід брати похідні. У цьому сенсі поліноміальна інтерполяція в порівнянні зі сплайн-інтерполяції має ту перевагу, що і інтерполяційний поліном, і похідні від нього однозначно є функціями безперервними і гладкими. Тому цікаво порівняти результати інтерполяції поліномом і сплайн-інтерполяції. Для цього побудуємо графіки відповідних інтерполяційних функцій.
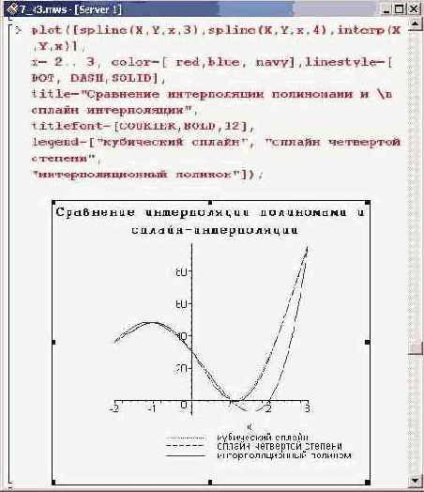
Можна бачити, що всі три графіка (сплайни третього і четвертого ступеня, а також інтерполяційний поліном четвертого ступеня) практично збігаються, особливо в лівій частині малюнка. Правда, інтерполяційний поліном є більш гладкою функцією в порівнянні з першими двома. При етрм у читача може виникнути питання: чому інтерполяційний поліном, ступінь якого дорівнює чотирьом, не збігається зі сплайн-функцією, побудованої на основі поліномів четвертого ступеня? Відповідь слід шукати в тих умовах, у тому числі визначається сплайн-функція. Так, при виконанні сплайн-інтерполяції поліномами ступеня m по п + 1 точкам задіяно п сплайн-поліномів. У кожному з цих поліномів слід визначити по т + 1 коефіцієнту, і всього отримуємо, таким чином, n (m + 1) невідомих коефіцієнтів. Рівність інтерполяційної функції у вузлових точках табличних значень задає п + 1 умов на невідомі коефіцієнти. Крім того, на внутрішніх вузлах (їх всього п-1) передбачається безперервність похідних до порядку т-1 включно, що дає, разом з безперервністю самої функції, (n-l + (m-l) (n-l)) = m (n-l) умов. Таким чином, на n (m + l) невідомих коефіцієнтів накладається (m (n-l) + (n + l)) = (n (m + l) - (m-l)) умов. Цього, зрозуміло, мало - необхідно ще т-1 умов. Їх, як правило, отримують, вимагаючи рівності нулю відповідного числа старших безперервних похідних на кордонах області інтерполяції. Це так званий природний вибір додаткових умов. В принципі, з математичної точки зору, їх можна вибирати довільним чином - в залежності від розв'язуваної задачі. Зокрема, умови ці можна підбирати так, щоб при інтерполяції сплайнами ступеня п в результаті виходив інтерполяційний поліном Лагранжа.