12. Теорема про суму кутів трикутника (формулювання і приклад).
1. У трикутнику один з кутів дорівнює 29 °, інший 91 °. Знайдіть його третій кут.
Рішення. Третій кут трикутника дорівнює
180 ° - (29 ° + 91 °) = 180 ° - 120 ° = 60 °.
2. Знайдіть гострі кути рівнобедреного прямокутного трикутника.
Рішення. З теореми про суму кутів трикутника випливає, що сума гострих кутів прямокутного трикутника дорівнює 180 ° - 90 ° = 90 °. Так як гострі кути в равнобедренном прямокутному трикутнику рівні, то кожен з них дорівнює 90 °. 2 = 45 °.
3. Знайдіть кути рівностороннього трикутника.
Рішення. З теореми про суму кутів трикутника випливає, що сума кутів рівностороннього трикутника дорівнює 180 °. Так як в рівносторонньому трикутнику всі кути рівні, то кожен з них дорівнює 180 °. 3 = 60 °.
13. Рішення трикутника за трьома сторонами.
Вирішити трикутник за трьома сторонами - це значить за трьома заданим сторонам трикутника знайти його кути.

Єдність розв'язку задачі випливає з ознаки рівності трикутників:
Якщо три сторони одного трикутника відповідно рівні трьом сторонам другого трикутника, то такі трикутники рівні.
14. Завдання по темі «Середня лінія трапеції».

15. Визначення синуса гострого кута прямокутного трикутника. Приклад його застосування для вирішення прямокутних трикутників.
Синусом гострого кута прямокутного трикутника називається відношення протилежного катета до гіпотенузи:
1. Дан прямокутний трикутник. Знайдіть: а) гіпотенузу с і катет Ь, якщо дані катет а й протилежні йому кут а;
б) катети трикутника а й Ь якщо дані гіпотенуза с і один з гострих кутів а (рис. 12).
2. На вершину гори йде канатна дорога довжиною 1,2 км, що становить кут 60 ° з висотою гори. Чому дорівнює висота гори?
Рішення. Позначимо довжину канатної дороги через с, висоту гори через Л, а кут між канатною дорогою і висотою гори через (3 (рис. 13).
Дано: з = 1,2 км, р = 60 °.
Рішення. З теореми про суму кутів трикутника випливає, що сума гострих кутів прямокутного трикутника дорівнює 90 °. Тому а = 30 °. Звідси
16. Властивість кутів рівнобедреного трикутника.
Трикутник називається рівнобедреним, якщо у нього дві сторони рівні. Ці рівні сторони називаються бічними сторонами, а третя сторона називається підставою трикутника.
[П] У трикутник кути при основі рівні.
Дано: ABC - рівнобедрений трикутник, АВ - підстава (рис. 14).
Довести: кут А = кут В.
Доведення. Трикутник САВ дорівнює трикутнику СВА за першою ознакою рівності

17. Завдання по темі «Подоба трикутників».

18. Завдання по темі «Паралелограм».
У трикутник вписаний паралелограм так, що кут паралелограма збігається з кутом при вершині трикутника, а вершина протилежного кута лежить на підставі. Доведіть, що периметр паралелограма є величина постійна для даного трикутника.

19. Визначення косинуса гострого кута прямокутного трикутника. Приклад його застосування для вирішення прямокутних трикутників.
Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи:
1. Дан прямокутний трикутник. Знайдіть:
а) гіпотенузу с і катет а, якщо дані катет видання та прилегла до нього кут а;
б) катети трикутника a і b, якщо дані гіпотенуза с і один з гострих кутів а (рис. 16).

2. Кут між сходами ескалатора і підлогою залу дорівнює 150 °. Яка довжина сходів ескалатора, якщо підошва сходи дорівнює 117м?

20. Ознака рівнобедреного трикутника.
Трикутник називається рівнобедреним, якщо у нього дві сторони рівні. Ці рівні сторони називаються бічними сторонами, а третя сторона називається підставою трикутника.
[П] Якщо в трикутнику два кути рівні, то він рівнобедрений.

Доведення. Так як в трикутнику два кути рівні, то рівні і сторони, що лежать проти цих кутів. Дійсно, якщо припустити, що одна із зазначених сторін більша за іншу, то кут, що лежить проти неї, буде більше кута, лежачого проти іншого боку, а це суперечить умові (тому, що дані кути рівні). Отже, в трикутнику дві сторони рівні, т. Е. Трикутник - рівнобедрений.
21. Завдання по темі «Подоба трикутників».
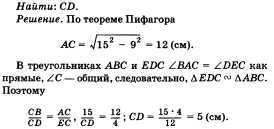
22. Завдання по темі «Прямокутник».
Сторони прямокутника дорівнюють 5 см і 4 см. Бісектриси кутів, прилеглих до більшої стороні, ділять протилежну сторону на три частини. Знайдіть довжини цих частин.

23. Визначення тангенса гострого кута прямокутного трикутника. Приклад його застосування для вирішення прямокутних трикутників.
Тангенсом гострого кута прямокутного трикутника називається відношення протилежного
катета до прилеглого:
1. Дан прямокутний трикутник. Знайдіть:
а) гіпотенузу с і катет Ь, якщо дані катет а й протилежні йому кут а;
б) гіпотенузу с і катет а, якщо дані катет ь і прилегла до нього кут а (рис. 20).

2. Під яким кутом падає на землю промінь сонця, якщо вертикально встромлений в землю жердину підноситься над землею на 18 м і відкидає тінь, рівну 6 73 (рис. 21)?
Позначимо довжину жердини через а, довжину тіні жердини через Ь, а кут, під яким на землю падає промінь сонця, через а.
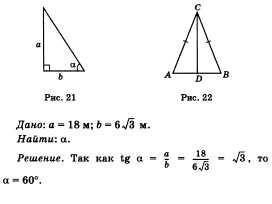
24. Властивість медіани рівнобедреного трикутника.
У трикутник медіана, проведена до основи, є бісектрисою і висотою.
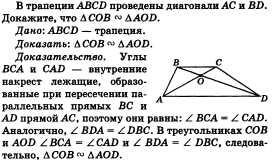
Дано: А АВС - трикутник, АВ - підстава, CD - медіана (рис. 22).
Довести: CD - бісектриса і висота.
Доведення. Трикутники CAD і CBD рівні але другою ознакою рівності трикутників (сторони АС і ВС рівні, так як АВС - рівнобедрений. Кути CAD і CBD рівні як кути при основі рівнобедреного трикутника. Сторони AD і BD рівні, оскільки D - середина відрізка АВ).
З рівності трикутників CBD і CAD слід рівність кутів:
Так як кути ACD і BCD рівні, то CD - бісектриса. Оскільки кути ADC і BDC суміжні і рівні один одному, вони прямі. Отже, відрізок CD є також висотою трикутника АВС. Теорема доведена.
Таким чином, встановлено, що бісектриса, медіана і висота рівнобедреного трикутника, проведені до основи, збігаються. Тому справедливі також наступні твердження:
1. Бісектриса рівнобедреного трикутника, проведена до основи, є медіаною і бісектрисою.
2. Висота рівнобедреного трикутника, проведена до основи, є медіаною і бісектрисою.
25. Завдання по темі «Подоба трикутників».
26. Завдання по темі «Ромб. Квадрат ».
Доведіть, що в ромб можна вписати коло.
Дано: ABCD - ромб, О - точка перетину діагоналей ромба.
Довести: Про - центр вписаного кола.
Доведення. Трикутники ABO, ADO, CBO і CDO - прямокутні (так як ABCD - ромб) і рівні по гіпотенузі і катету. Отже, і висоти OF і ОЕ проведені з вершин пря мих кутів, рівні. Значить, підстави висот лежать на окружності з центром О. Так як висоти, проведені з вершин прямих кутів, перпендикулярні сторонам ромба, то окружність з центром Про - точкою перетину діагоналей ромба - і радіусом, рівним відстані від точки О до сторін ромба, стосується сторін ромба. Отже, в ромб можна вписати коло.
27. Теорема косинусів. Приклад її застосування для вирішення трикутників.
Квадрат будь-якої сторони трикутника дорівнює сумі квадратів катетів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.

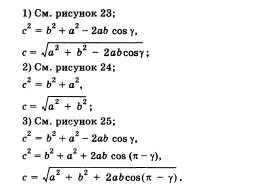

28. Коло, вписане в трикутник.
Коло називається вписаною в трикутник, якщо вона стосується всіх його сторін.
[П] Теорема про центр кола, вписаного в трикутник.
Центр кола, вписаного в трикутник, є точкою перетину його бісектрис.
Дано: АВС - даний трикутник; Про - центр вписаного в нього кола; D, Е і F - точки дотику кола зі сторонами трикутника (рис. 27).
Довести: Про - точка перетину биссектрис.
Доведення. Прямокутні трикутники AOD іАОЕ рівні по гіпотенузі і катету. У них гіпотенуза ОА - загальна, а катети OD і ОЕ рівні як радіуси. З рівності трикутників випливає рівність кутів OAD і ОАЕ. А це означає, що точка О лежить на бісектрисі трикутника, проведеної з вершини А. Точно так само доводиться, що точка О лежить на двох биссектрисах трикутника.
[А] Теорема про кола, вписаного в трикутник.
У будь-який трикутник можна вписати коло.
Дано: A ABC - даний трикутник, О - точка перетину биссектрис, М, L і К - точки дотику кола зі сторонами трикутника (рис. 28).
Довести: Про - центр кола, вписаного в АВС.
Доведення. Проведемо з точки Про перпендикуляри OK, OL і ОМ відповідно до сторін АВ, ВС і СА (див. Рис. 28). Так як точка Про рівновіддалена від сторін трикутника ABC, то Про К = OL = = ОМ. Тому коло з центром О радіуса ОК проходить через точки K L M. Сторони трикутника ABC стосуються цієї окружності в точках K, L, М, так як вони перпендикулярні до радіусів ОК, OL і ОМ. Значить, коло з центром О радіуса ОК є вписаною в трикутник ABC. Теорема доведена.
Зауваження. Відзначимо, що в трикутник можна вписати тільки одне коло. Справді, припустимо, що в трикутник можна вписати дві окружності. Тоді центр кожного кола рівновіддалений від сторін трикутника і, отже, збігається з точкою О перетину биссектрис трикутника, а радіус дорівнює відстані від точки О до сторін трикутника. Отже, ці кола співпадають.
29. Завдання по темі «Паралельні прямі».

30. Завдання по темі «Теорема Піфагора».
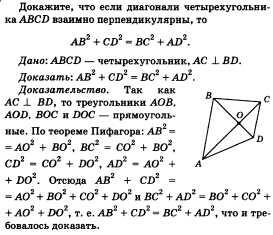
Доведіть, що якщо діагоналі чотирикутника ABCD взаємно перпендикулярні, то
Схожі роботи:
Організація узагальнюючого повторення на уроках геометрії в 7 класі
Курсова робота >> Педагогіка
Вивчення теми Трикутники в курсі геометрії 7-9 класів середньої школи
Курсова робота >> Педагогіка
по темі "Трикутники" для 7-9 класів п. 1 Узагальнюючий урок по темі "Ознаки рівності трикутників" (За підручником Погорєлова А.В. Геометрія. результати їх роботи, заохочуються кращі відповіді. Методичні рекомендації: Кількість докази записаного.
Відповіді на екзаменаційні питання з історії Росії 11 клас. Для зручності користування запитання та відповіді розміщено в хронологічному. університету Н. І. Лобачевський стояв біля витоків неевклідової геометрії. У 1839 р в Пулково під Петербургом В. Я. Струве.
Відповіді на екзаменаційні питання з історії Росії 9 клас. Джерела: Відповіді на питання / квитки по. І. Лобачевський стояв біля витоків неевклідової геометрії. У 1839 р в Пулково під. профспілки для робітників, комсомол - для молоді, піонерська організація - для.
Відповіді на питання по філософії для вступників до аспірантури
Відповіді на питання по філософії для вступників до аспірантури природних. приноситься в жертву механічному, а геометрія проголошується головною наукою. Важливою заслугою. другий план. У німецькій клас іческой філософії натурфілософія знову висувається.