1.Собрать і вивчити матеріал.
2.Найті дивовижне в ряді натуральних чисел.
3.Открить будь-які закономірності і властивості в ряду чисел.
4.Обобщіть отримані дані і сформулювати висновок.
Результати проведеного дослідження
Прості і складені числа
Натуральне число називається простим, якщо воно має тільки два дільника: одиницю й саме це число. Натуральне число називають складеним, якщо воно має більше двох дільників. Число 1 має тільки один дільник: саме число. Тому його не відносять ні до складових, ні до простих чисел. Першими десятьма простими числами є: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Будь-яке складене число можна розкласти на два множники, кожен з яких більше 1. Просте число так розкласти на множники не можна. Твір двох простих чисел може бути простим число, якщо одне з чисел дорівнює 1, а інше є простим числом. Всі прості числа, великі 2, непарні.
Нерозгадана таємниця простих чисел
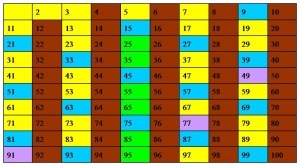
Таємниця простих чисел-це їх розподіл між іншими числами: довільне, без будь-якого порядку. Прості числа в ряду натуральних чисел зустрічаються неравномерно- в одних частинах ряду їх більше, в інших - менше. Математики роками намагалися знайти цей порядок, але безуспішно. А відсутність порядку означає, що прості числа потрібно відшукувати одне за іншим. Малі прості числа легко знайти за допомогою так званого «Решета Ерастофен». У таблицю вписуємо всі числа до 100 (1 не включається: вона не є простим числом). Викреслюємо всі парні числа, крім 2. Потім викреслюємо всі числа, що діляться на 3, крім 3. Числа, що діляться на 4, вже викреслені, тому переходимо до 5, потім до 7. Всі залишилися числа (жовті клітини) - прості.
Прості числа називають цеглинами в побудові математики, так як всі інші числа можна сформувати, перемножая прості. Наприклад, 55 = 5 × 11 75 = 3 × 5 × 5 39 = 3 × 13 65 = 5 × 13 221 = 13 × 17 73 939 133 - дивовижне просте число. Можна видалити з його кінця будь-яке число цифр, і час, що залишився число теж буде простим. Це найбільше відоме число, що володіє такою властивістю.
Сверхсоставние числа (Книга «Я пізнаю світ»)
Людині властиво вишукувати най-най у всьому, з чим він має справу, «Книга рекордів Гінесса» - тому підтвердження. А яке число найбільше? Такого числа немає, оскільки будь-яке число ми можемо збільшити, додавши до нього одиничку. Пошукаємо чемпіонів серед натуральних чисел за кількістю дільників. Найменше різних дільників у числа 1, всього один - сама одиничка. У всіх простих чисел по два подільника - саме число і одиничка. А у якого натурального числа найбільше дільників? Ясно, що такого числа немає, так як помноживши натуральне число, скажімо, на два, ми збільшуємо кількість його різних дільників. Сверхсоставним числом будемо називати натуральне число, яке має більше подільників, ніж кожен з великих його натуральних чисел. Яке сверхсоставное число буде найменшим? Число 1 має рівно один дільник. Числа 2 і 3 мають рівно по два подільника, так як вони прості. Число 4 має три дільника. Число 6 має чотири дільники: 1, 2, 3 і 6. Здавалося б, що наступним має йти число з п'ятьма делителями. Найменша таке число 16, його подільники 1, 2, 4, 8 і 16. Але його визначило число 12, у якого шість дільників: 1, 2, 3, 4, 6 і 12. Тому число 16 Не стало сверхсоставним, а їм стало число 12. Наступне число, яке є сверхсоставним буде число 30 з вісьмома делителями. Потім, 36, 40, 54, 56 все з вісьмома делителями, 48 з десятьма делителями, число 60 має дванадцять дільників і тільки число 64 має рівно сім дільників, а значить числа 36, 40, 48, 54, 56 і 60 є свехсоставнимі числами . Взаємно прості числа
Натуральні числа, називають взаємно простими, якщо їх найбільший спільний дільник дорівнює 1.
Так називаються прості числа, що відрізняються один від одного на 2. У першому десятку простих чисел такими парами будуть 3 і 5, 5 і 7, 11 і 13, 17 і 19 До числа невирішених досі завдань відноситься проблема «близнюків». Невідомо, обірветься чи коли-небудь цей список або ж він нескінченний, як і ряд простих чисел. дружні числа
Натуральне число будемо називати хорошим, якщо воно ділиться на суму цифр самого числа. За визначенням хороших чисел все цифри від 1 до 9 є хорошими числами. Найменше двозначне число 10, так як воно ділиться на число, що дорівнює (1 + 0). Наступним числом є 12, тому що 12 ділиться на 1 + 2, як вже ми довели це ж число є і сверхсоставним. 13 - не є добре число, т. К. 13 не ділиться на (1 + 3); 14 - не є добре число, т. К. 14 не ділиться на (1+ 4); 15 - не є добре число, т. К. 15 не ділиться на (1+ 5); 16 - не є добре число, т. К. 16 не ділиться на (1+ 6); 17 - не є добре число, т. К. 17 не ділиться на (1+ 7); 18 - гарне число, тому що 18 ділиться на (1+ 8); 19 - не є добре число, тому що 19 не ділиться на (1+ 9); Хороші числа: 10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54 і т.д. Як ми бачимо, всі хороші числа є складовими числами.
Досконалим числом називають натуральне число, яке дорівнює сумі дільників цього числа, менших самого числа. Піфагор (VI ст до н.е.) і його учні вивчали питання про подільність чисел. Число, яка дорівнює загальній кількості всіх його подільників (без самого числа), вони називали досконалим числом. Наприклад, 6 = 1 + 2 + 3, де числа 1, 2 і 3 є дільниками числа 6. 28 = 1 + 2 + 4 + 7 +14, де числа 1, 2, 4, 7 і 14 подільники числа 28. Наступні вчинені числа - 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248, де числа 1, 2, 4, 8, 16, 31, 62, 124 і 248 є дільниками числа 496 Піфагорійці знали тільки перші три скоєних чисел. Четверте досконале число - 8128 стало відомо в 1 столітті нашої ери. П'яте - 33550336 було знайдено в XV столітті нашої ери. Вчинені числа тісно пов'язані з простими числами Мерса, тобто з числами виду 2m - 1. Ще Евклід встановив, що число n = 2m-1 (2m - 1) є досконалим, якщо 2m - 1 просте число. До 1983 року було відомо вже 27 скоєних чисел і всі знайдені вчинені числа є парними числами. Перші 23 з цих чисел відповідають значенням m: 2,3,5, 7., 7,13,17,19,31,61, 89,107,127,521,607,1279,2203,2281,3271,4219,4423,9689,9941,11213. Але до сих пір вчені не знають, чи є непарні досконалі числа, чи є найбільше досконале число.
Трикутні числа Піфагор (IY століття до нашої ери) і його учні розглядали послідовності, пов'язані з геометричними фігурами. Підраховуючи число гуртків в трикутниках, квадратах, п'ятикутник вони отримали: - послідовність (А2) трикутних чисел 1, 3, 6, 10, 15, ... виходить таким чином: 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, 1 + 2 + 3 + 4 + 5, ..., - послідовність (b2) квадратних чисел 1, 4, 9, 16, 25, .... отримують у такий спосіб: 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7, 1 + 3 + 5 + 7 + 9, ..., n 2 - послідовність (c2) п'ятикутних чисел 1, 5, 12 , 22, 35, ... виходить таким чином: 1, 1 + 4, 1 + 4 + 7, 1 + 4 + 7 + 10,4 + 7 + 10 + 13, ...,
Числа-самородки Візьмемо числа 5, 10, 11, 13, 17, 25, .... Всі числа, крім 5, сформовані за єдиним правилом. До числа додається сума його цифр. Так, 5 + 5 = 10, 10 + 1 = 11, 11 + 2 = 13, 13 + 4 = 17, ... Все починається з числа 5. Число 5 виявилося як би самородком. Однозначні самородки виявляються відразу 1, 3, 5, 7 і 9. З двозначних найменше 20, потім 31, ... Є колекція «самородків» і серед багатозначних чисел. Наприклад, 132, 143, 233, 929, 1952 і т.д.
Число називається симетричним, якщо існує пряма (або центр симетрії), що переводить це число в себе. Якщо розглянути всі десять цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, то можна помітити: Цифра 8 має тільки вертикальну вісь симетрії l і є симетричним числом щодо цієї вертикальної осі (прямий). Цифра 0 має дві осі симетрії, вертикальну і горизонтальну, і один центр симетрії (цей центр - точка перетину вертикальної і горизонтальної осей симетрії).
Цифри 8 і 0 є симетричними, значить, все симетричні числа будуть складені з цих цифр. Найменшим і єдиним двозначним числом є число 88. Віссю симетрії числа 88 є пряма m, яка переводить першу вісімку на другу. Наступним симетричним числом є число 808, що має вертикальну вісь симетрії p, другим симетричним тризначним числом є число 888.
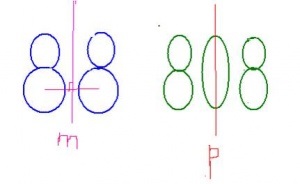
Чотиризначні симетричні числа: 8008, 8888. П'ятизначні симетричні числа: 80008, 80808, 88088, 88888.
Числа оточують нас і всіляко допомагають нам в наших справах. Вони - інструмент для рахунку. Без чисел ми не знали б, який сьогодні день і котра година. В наші дні числа всюди, і вони потрібні нам завжди. Важко уявити, у що перетворився б світ, якби у нас не було чисел! Число - основне поняття математики, яке склалося під час тривалого історичного розвитку. Поняття числа розвивалося в тісному зв'язку з вивченням величин; цей зв'язок зберігається і тепер. У всіх розділах сучасної математики доводиться розглядати різні величини і користуватися числами. Потреба рахунку предметів привела до виникнення поняття натурального числа. Всі народи, котрі володіли писемністю, володіли поняттям натурального числа. Існує велика кількість визначень поняття «число». Перше наукове визначення числа дав Евклід у своїх «Засадах»: «Одиниця є те, відповідно до чого кожна з існуючих речей називається однієї. Число є безліч, складене з одиниць ». Раніше Евкліда Аристотель дав таке визначення: «Число є безліч, яке вимірюється за допомогою одиниць». Ще Фалес - родоначальник грецької стихійно-матеріалістичної філософії - учив, що «число є система одиниць». Давньогрецький математик Піфагор так говорив про числі: «Число це закон і зв'язок світу, що панує над богами і смертними», «Сутність речей є число, яке вносить у все єдність і гармонію», «Все є число». У своїй «Загальній арифметиці» (1707 р) великий англійський фізик, механік, астроном і математик Ісаак Ньютон пише: «Під числом ми маємо на увазі не тільки безліч одиниць, скільки абстрактне відношення якої-небудь величини до іншої величини такого ж роду, взятої за одиницю . Число буває трьох видів: ціле, дробове і ірраціональне. Ціле число є те, що вимірюється одиницею; дробове - кратною частиною одиниці, ірраціональне - число, що не порівнянне з одиницею ». Вивченню дивовижних особливостей натуральних чисел немає кінця. Нашою групою було досліджено ряд натуральних чисел, що володіють цікавими особливостями, розглянуті прості і складені числа, сверхсоставние числа, вчинені числа і хороші числа, числа-близнюки, дружні числа, особливі числа, симетричні числа. В результаті вивчення цієї теми вдалося поглиблено вивчити шкільні теми, прості і складені числа. Ми познайомилася з особливими двозначними числами, у яких твір двозначних чисел не змінює своєї величини, якщо переставити їх цифри. До дивним числах відносяться симетричні числа. Вивчаючи ряд натуральних чисел, можна знайти багато особливостей натуральних чисел. В цілому поставлені завдання виконані. Давньогрецький математик Евклід (III ст. До н.е.) у своїй книзі «Начала», колишній протягом двох тисяч років основним підручником математики, довів, що простих чисел нескінченно багато, тобто за кожним простим числом є ще більше просте число. Наша гіпотеза виявилася вірною, вказати найбільше просте число, складене, вчинене, симетричне неможливо. Під час вивчення цієї теми вдалося поглиблено вивчити шкільні теми, прості і складені числа. Ознайомитися зі сверхсоставнимі числами, з особливими двозначними числами, тобто твір двозначних чисел не змінює своєї величини, якщо переставити їх цифр. Нове до дивних числах - ці хороші і симетричні числа, числа-самородки. Тут зупиняється рух по натуральному ряду. Чи не занадто багато уваги приділено початковим крокам в математику? Відповіддю на це міг би послужити відомий афоризм німецького математика Леопольда Кронекера (1823-1891): "Бог створив натуральні числа, все інше - справа рук людських".
Корисні ресурси
- www.mersenne.org
- Босова Л.Л. Інформатика: підручник 6 класу, глава «Матеріал для допитливих»
- Алгебра 9 клас під ред. Макаричева М.Н..Глейзер Г. І. «Історія математики в школі», М: Просвещение, 1982 р
Книга для учнів «Я пізнаю світ»
- «Математична енциклопедія» / Гол. ред. І.М. Віноградов.-М.: Радянська енциклопедія
- Підручник Математика 6 класу під редакцією Н. Я. Виленкина