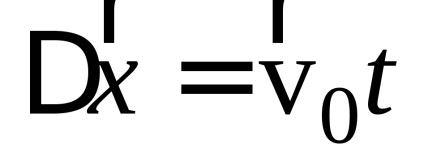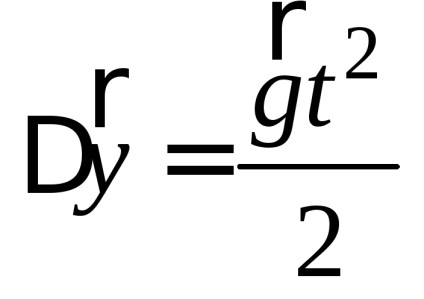Вільний рух тіл, кинутих під кутом до горизонту приклади розв'язання задач

1. Тіло кинули з поверхні Землі під углом = 60к горизонту з початковою швидкістю v0 = 20 м / с. Нехтуючи опором повітря, знайти:

а) швидкість тіла через t = 2 с після початку руху;

б) час t1. через яке швидкість становитиме з горизонтом угол = 30;

в) час польоту тіла Т до падіння на Землю;

г) максимальну висоту підйому Н і дальність полетаL;

д) рівняння траєкторії y (x), гдеx іy - координати тіла.

а

) Вибираємо систему отсчетаx 0y, показану на малюнку. За своїм характером цей рух є рух з постійним прискореннямТому закон зміни швидкості з плином часу має вигляд:

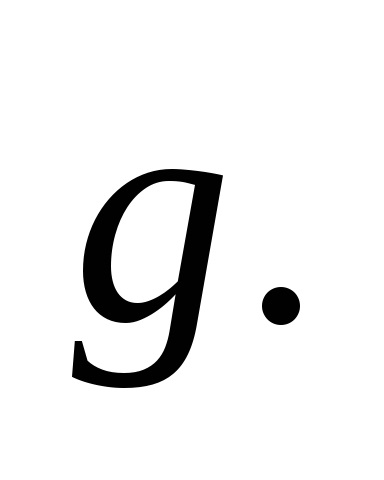
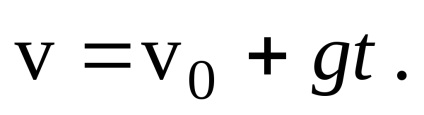
Знайдемо проекції вектора швидкості на осі координат, спроектувавши це рівняння на осі x іy:

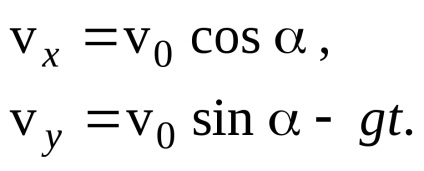
З зв'язку між модулем вектора і його проекціями на декартові осі отримаємо:

б) Якщо - кут між вектором швидкості і горизонтальною віссю в певний момент временіt1. то:

в) Запишемо закон руху тіла в векторному вигляді, врахувавши, що в початковий момент тіло знаходилося на початку координат.

тут

- радіус-вектор тіла в момент часу t.

Спроектуємо це рівняння на вісь y:

Знайдемо час польоту тіла Т з умови, що в цей момент коордінатаy = 0:

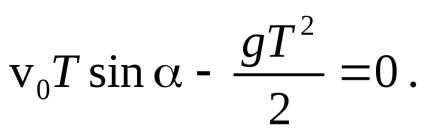
Один з коренів отриманого рівняння Т1 = 0 відповідає початковому положенню тіла, інший корінь дає час польоту тіла:

г) Спроектуємо рівняння (1) на вісь x:

Знайдемо дальність польоту тіла L з умови L = x (T):

Для того, щоб визначити максимальну висоту підйому Н. знайдемо час польоту тіла в найвищу точку траєкторії з умови, що в цей момент временіТ вектор швидкості

направлений горизонтально і, отже, проекція швидкості на осьy vy = 0, тобто

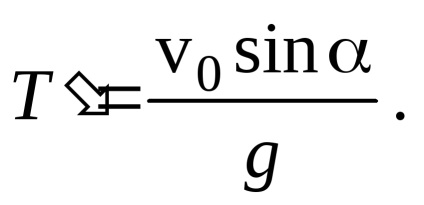
Зауважимо, що час підйому Т дорівнює половині часу полетаТ. Отже, час підйому одно часу спуску.

д) Закон руху в координатної формі, визначається співвідношеннями (2) і (3), по суті задає рівняння траєкторії через параметр t. Виключивши цей параметр, отримаємо рівняння траєкторії в явному вигляді:

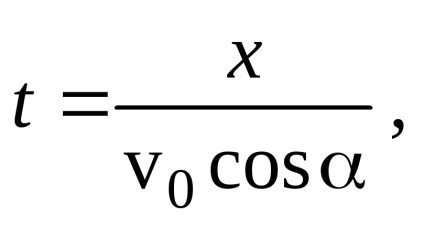
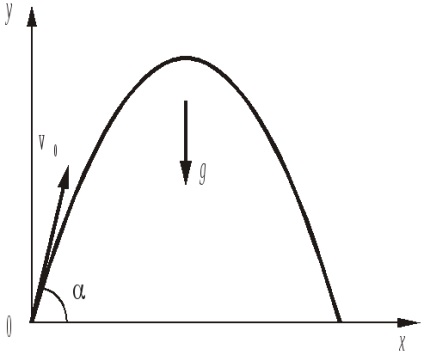
З (4) випливає, що траєкторія тіла, кинутого під кутом до горизонту, являє собою параболу, гілки якої спрямовані вниз (коефіцієнт при x 2 негативний). Парабола проходить через початок координат (один з коренів уравненіяy (x) = 0 дорівнює нулю).

2. Літак летить на висотеh = 500 м по горизонтальній прямій з швидкістю v0 = 100 м / с. Льотчик повинен скинути бомбу в ціль, що лежить попереду літака. Під яким угломк вертикалі він повинен бачити мету в момент скидання бомби?

Р

ешеніем. Рух бомби можна розглядати як накладення двох рухів, одне з яких відбувається по горизонталі з постійною швидкістю v0. а інше являє собою вільне падіння з нульовою початковою швидкістю (див. рис.).

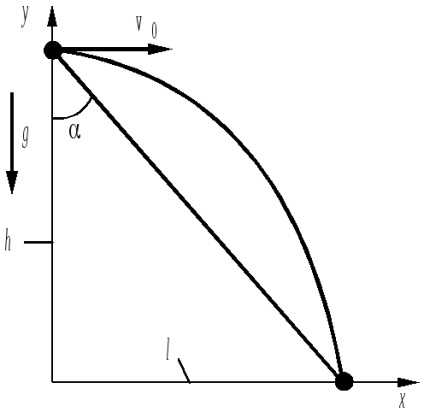
Шуканий кут определяется очевидним співвідношенням:

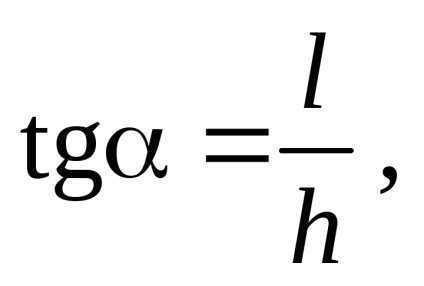
де l - дальність польоту по горизонталі. Ця величина равнаl = v0t. гдеt - час польоту бомби знаходиться з умови

;

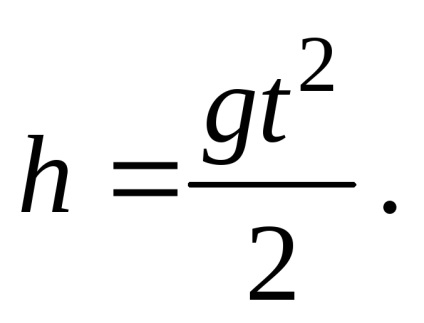
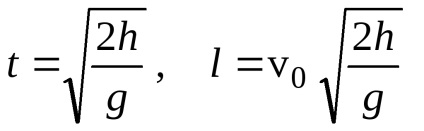
3. Під яким угломк горизонту слід кинути камінь зі скоростьюv0 = 20 м / с, щоб він пролетів по горизонталі до падіння на землю відстань

? Опір повітря знехтувати.

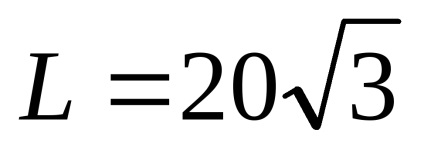
Рішення. Запишемо співвідношення між дальністю полетаL. початкової скоростьюv0. угломі прискоренням вільного паденіяg (див. (3) завдання 1 цього розділу):

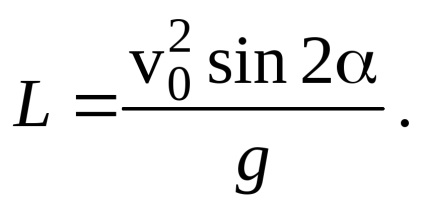
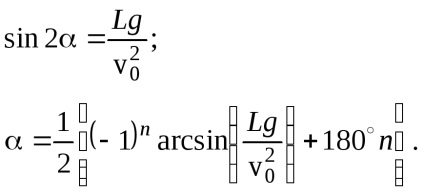
Тут n - цілі числа, значення яких знайдемо з очевидного умови:

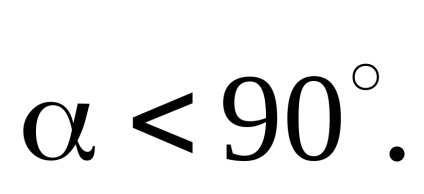
Нехай n = 0. Тоді

Пріn = 1

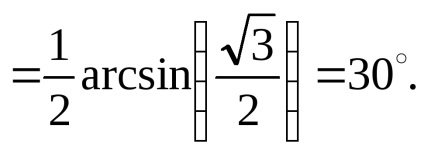
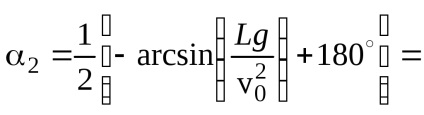
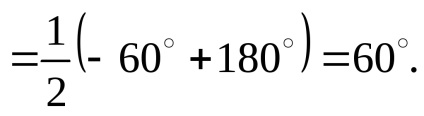
При інших значеннях n угол> 90. Отже, шукані кути рівні:

4. Камінь кинули горизонтально з великої висоти зі швидкістю

м / с. визначити черезз:

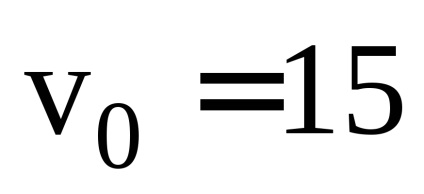
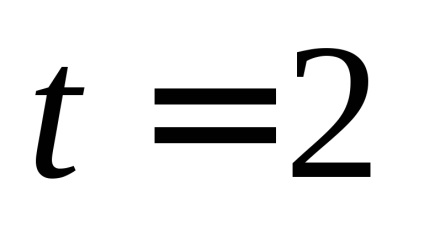
а) швидкість

каменю і модуль збільшення вектора його швидкості;

б) модуль вектора переміщення каменю.

Рішення. а) Відповідно до виразом (1.12) швидкість каменю дорівнює

,

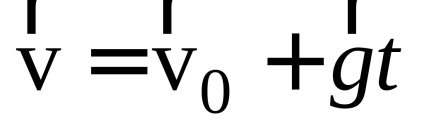
де

- прискорення вільного падіння. Знайдемо побудовою швидкість(Див. Рис.). З отриманого трикутника швидкостей знаходимо:

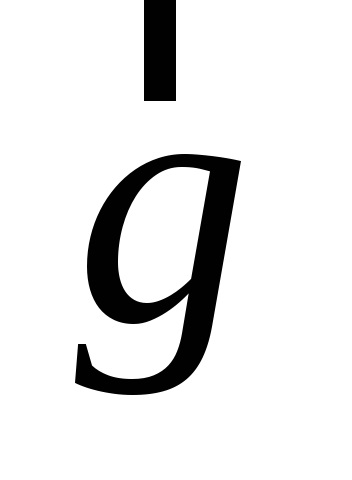
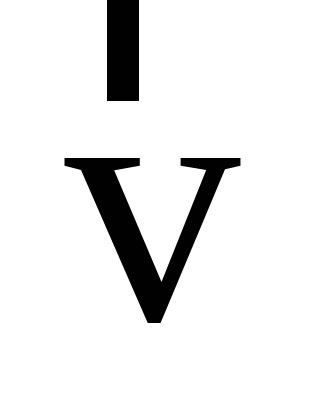
За визначенням і

м / с.

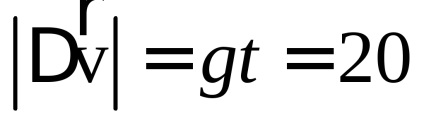
б) Вектор переміщення дорівнює

,

де

, а, а його модуль