Завдання. Вирішити графічно задачу лінійного програмування, визначивши екстремальне значення цільової функції:
Побудуємо область допустимих рішень, тобто вирішимо графічно систему нерівностей. Для цього побудуємо кожну пряму і визначимо півплощини, задані нерівностями (півплощини позначені штрихом).
Побудуємо рівняння 3x1 + x2 = 9по двох точках.
Для знаходження першої точки прирівнюємо x1 = 0. Знаходимо x2 = 9. Для знаходження другої точки прирівнюємо x2 = 0. Знаходимо x1 = 3. З'єднуємо точку (0; 9) з (3; 0) прямою лінією. Визначимо напівплощина, що задається нерівністю. Вибравши точку (0; 0), визначимо знак нерівності в півплощині: 3 • 0 + 1 • 0 - 9 ≤ 0, тобто 3x1 + x2 - 9≥ 0 в півплощині вище прямої.
Побудуємо рівняння x1 + 2x2 = 8по двох точках.
Для знаходження першої точки прирівнюємо x1 = 0. Знаходимо x2 = 4. Для знаходження другої точки прирівнюємо x2 = 0. Знаходимо x1 = 8. З'єднуємо точку (0; 4) з (8; 0) прямою лінією. Визначимо напівплощина, що задається нерівністю. Вибравши точку (0; 0), визначимо знак нерівності в півплощині: 1 • 0 + 2 • 0 - 8 ≤ 0, тобто x1 + 2x2 - 8≥ 0 в півплощині вище прямої.
Побудуємо рівняння x1 + x2 = 8по двох точках.
Для знаходження першої точки прирівнюємо x1 = 0. Знаходимо x2 = 8. Для знаходження другої точки прирівнюємо x2 = 0. Знаходимо x1 = 8. З'єднуємо точку (0; 8) з (8; 0) прямою лінією. Визначимо напівплощина, що задається нерівністю. Вибравши точку (0; 0), визначимо знак нерівності в півплощині: 1 • 0 + 1 • 0 - 8 ≤ 0, тобто x1 + x2 - 8≤ 0 в півплощині нижче прямої.
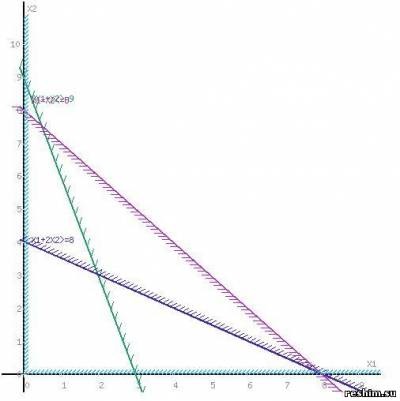
Перетином напівплощин буде область, координати точок якого задовольняють умові нерівностей системи обмежень задачі.
Позначимо кордону області багатокутника рішень.
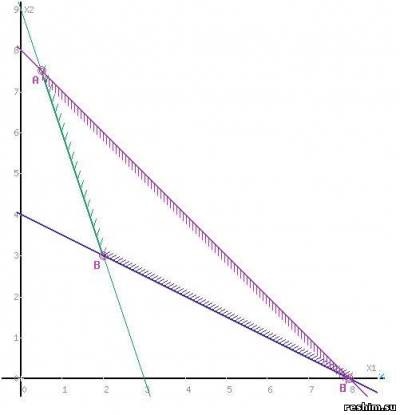
Перевірити вірність побудови графіків функцій можна за допомогою калькулятора
Розглянемо цільову функцію завдання F = 4x1 + 6x2 → min.
Побудуємо пряму, що відповідає значенню функції F = 0: F = 4x1 + 6x2 = 0. Вектор-градієнт, складений з коефіцієнтів цільової функції, вказує напрямок мінімізації F (X). Початок вектора - точка (0; 0), кінець - точка (4; 6). Будемо рухати цю пряму паралельним чином. Оскільки нас цікавить мінімальне рішення, тому рухаємо пряму до першого торкання позначеної області. На графіку ця пряма позначена пунктирною лінією.
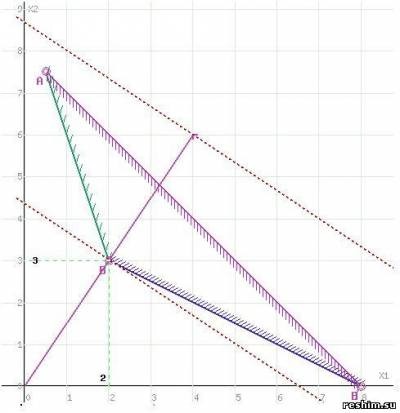
Пряма F (x) = 4x1 + 6x2 перетинає область в точці B. Так як точка B отримана в результаті перетину прямих (1) і (2). то її координати задовольняють рівнянням цих прямих:
3x1 + x2 = 9
x1 + 2x2 = 8
Вирішивши систему рівнянь, отримаємо: x1 = 2, x2 = 3
Звідки знайдемо мінімальне значення цільової функції:
F (X) = 4 * 2 + 6 * 3 = 26