Контрольна робота №3
Для економічних спеціальностей заочної форми навчання
1. Кинуті два гральних кубика. Яка ймовірність, що сума очок буде дорівнює 7?
2. Припустимо, що для однієї торпеди ймовірність потрапити в ціль дорівнює 0,7. Яка ймовірність того, що три торпеди потоплять корабель, якщо для потоплення досить одного попадання торпеди в ціль?
3. Складальник отримав 3 коробки деталей, виготовлених заводом №1, і 2 коробки деталей, виготовлених заводом №2. Імовірність того, що деталь заводу №1 стандартна дорівнює 0,8, а заводу №2 - 0,9. Складальник навмання витягнув деталь з випадково вибраної коробки. Знайти ймовірність того, що витягнута стандартна деталь.
4. Вирішити завдання, іспользуяформулу Бернуллі ітеореми Муавра-Лапласа.
а) Надсилаючи звіт про проблеми ймовірність спотворення одного знака дорівнює 0,1. Яка ймовірність того. що повідомлення з 10 знаків містить не більше 3 спотворень?
б) Було посаджено 400 дерев. Імовірність того, що окреме дерево приживеться дорівнює 0,8. Знайти ймовірність того, що число прижилися дерев: 1) дорівнює 300, 2) більше 310, але менше 330.
5. Дан перелік можливих значень дискретної величини: x1 = -2, x2 = 1, x3 = 4, а також дані математичне очікування цієї велічіниM [X] = 2,5 і її квадратаM [X 2] = 10,3. Знайти закон розподілу випадкової величини.
6.Непреривная випадкової величини задана функцією розподілу
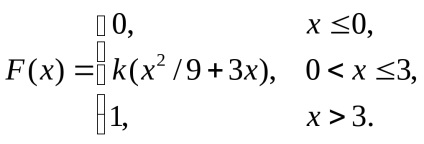
Знайти: а) параметр k; б) математичне сподівання; в) дисперсію.
7. Відомі математичне ожіданіеа = 10 і середнє квадратичне отклоненіе = 4нормально розподілу випадкової величини. Знайти ймовірність: а) попадання цієї величини в заданий інтервал (5, 9); б) відхилення цієї величини від математичного очікування не більше, ніж на.
8. З генеральної сукупності витягнута вибірка, яка представлена у вигляді інтервального варіаційного ряду. а) Припускаючи, що генеральна сукупність має нормальний розподіл, побудувати довірчий інтервал для математичного очікування з довірчою вероятностью = 0,95. б) Обчислити коефіцієнти асиметрії та ексцесу, використовуючи спрощений метод обчислень, і зробити відповідні припущення про вид функції розподілу генеральної сукупності. в) Використовуючи критерій Пірсона, перевірити гіпотезу про нормальність розподілу генеральної сукупності при рівні значімості = 0,05.
Вища математика
Контрольна робота №3
Для економічних спеціальностей заочної форми навчання
варіант 10
1. П'яти польовим радіостанціям дозволено під час навчань працювати на 6 радіохвилях. Вибір хвилі на кожній станції проводиться навмання. Знайти ймовірність того, що будуть використані різні радіохвилі.
3. У першому ящику міститься 20 деталей, з них 15 стандартних; у другому - 30 деталей, з них 24 стандартних; в третьому - 10 деталей, з них 6 стандартних. Знайти ймовірність того, що навмання витягнута деталь з навмання взятого ящика - стандартна.
4. Вирішити завдання, іспользуяформулу Бернуллі ітеореми Муавра-Лапласа.
а) Імовірність появи деякої події в кожному з 5 незалежних дослідів дорівнює 0,2. Визначити ймовірність появи цієї події по крайней мере 3 рази.
б) Схожість насіння даного сорту рослин становить 90%. Знайти ймовірність того, що з 900 посаджених насіння число пророслих буде: 1) дорівнює 800, 2) укладено між 805 і 820.
5.Діскретная випадкової величини має тільки два можливих значення: x1 іx2. прічемx1 6.Непреривная випадкової величини задана функцією розподілу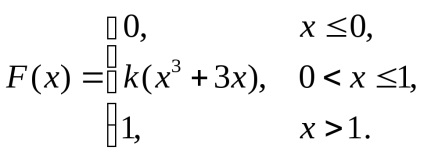
Знайти: а) параметр k; б) математичне сподівання; в) дисперсію.
7. Відомі математичне ожіданіеа = 9 і середнє квадратичне отклоненіе = 4нормально розподілу випадкової величини. Знайти ймовірність: а) попадання цієї величини в заданий інтервал (2, 10); б) відхилення цієї величини від математичного очікування не більше, ніж на.
8. З генеральної сукупності витягнута вибірка, яка представлена у вигляді інтервального варіаційного ряду. а) Припускаючи, що генеральна сукупність має нормальний розподіл, побудувати довірчий інтервал для математичного очікування з довірчою вероятностью = 0,95. б) Обчислити коефіцієнти асиметрії та ексцесу, використовуючи спрощений метод обчислень, і зробити відповідні припущення про вид функції розподілу генеральної сукупності. в) Використовуючи критерій Пірсона, перевірити гіпотезу про нормальність розподілу генеральної сукупності при рівні значімості = 0,05.