Визначення афінних перетворень
Давайте поговоримо про розтягненнях і сжатіях плоских фігур.
Якщо розтягнути вздовж якогось напрямку коло, то вийде лекальна крива - еліпс.
Якщо розтягнути квадрат в напрямку, паралельному одній парі сторін, то вийде прямокутник. Якщо ж квадрат розтягнути або стиснути в напрямку його діагоналі, то вийде ромб.
Але що таке розтягування і стиснення? Як їх строго визначити?
Розтягування і стиснення, про які ми будемо говорити, в певному сенсі, рівномірні.
Ця рівномірність означає, що всі шматочки площині будуть розтягуватися (стискатися) однаково.
Крім того, коли ми розтягуємо (стискаємо) квадрат, його боку - відрізки залишаються відрізками.
Такі рівномірні розтягування (стиснення) називаються аффіннимі перетвореннями.
Перетворення площини називається аффінним. якщо воно взаємно однозначно і способом будь-якої прямої є пряма. Перетворення називається взаємно однозначним. якщо воно різні точки переводить в різні, і в кожну точку переходить якась точка.
Нагадаємо, що перетворення - це відображення безлічі на саме себе. Відображення називається взаімооднозначном (биективное), якщо різні елементи переходять в різні, і в кожен елемент, якийсь елемент переходить.
Окремим випадком афінних перетворень є просто руху (без будь-якого стиснення або розтягування). Рухи - це паралельні переноси, повороти, різні симетрії і їх комбінації.
Інший важливий випадок афінних перетворень - це розтягування і стиснення відносно прямої.
На малюнку 1 показані різні рухи площині з намальованим на ній будиночком. А на малюнку 2 показані різні аффінниє перетворення цієї площини.
Малюнок 1. Приклади рухів.
Малюнок 2. Приклади афінних перетворень.
Позначимо безліч рухів площині як, а безліч афінних перетворень як. Тоді вірно наступне твердження.
Безліч рухів є підмножина безлічі афінних перетворень.
Це здається очевидним. Давайте зрозуміємо, що нам власне потрібно довести. Для цього потрібно ще раз подивитися на визначення руху та афінних перетворень. Потрібно довести, що будь-який рух є аффінним. Тобто потрібно показати, що при русі різні точки переходять в різні, і образ будь-якої прямої є пряма.
Це інтуїтивно зрозуміло - при русі фігури взагалі не міняють своєї форми і розмірів, а змінюють лише своє становище на площині. Також і прямі будуть зберігати свою форму - залишатися прямими. Рух можна представляти як переміщення листка паперу з малюнком по парті. При русі різні точки залишаються різними, оскільки відстані зберігаються. Якщо точки були «розділені» деякою відстанню, то і після руху вони будуть «розділені» цим же відстанню.
[Ред] Розтягнення і стиснення
Визначення 3.Растяженіем площині відносно прямої з коефіцієнтом називається перетворення площини, при якому кожна точка переходить в таку точку, що відстань від прямої до в раз більше, ніж до точки, і проекція точок і на пряму збігаються. Якщо коефіцієнт позитивний, то точки і лежать по одну сторону від прямої, якщо негативний - то по різні.
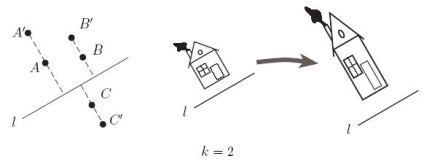
Малюнок 3. Стиснення і розтягування відносно прямої.
Давайте доведемо, що розтягнення (стиснення) відносно прямої є аффінним перетворенням. По-перше, ці перетворення взаємно однозначно. Щоб довести це зауважимо, що для кожного стиснення є розтягнення, яке всі крапки повертає на свої місця, і навпаки, для кожного розтягування є повертає все на свої місця стиснення. А зараз скористаємося теоремою:
Якщо перетворення назад перетворенню, а перетворення назад перетворенню, то і взаємно однозначні перетворення.
Перетворення називається зворотним до перетворення, якщо перетворення, застосоване після перетворення, всі крапки повертає на свої місця. Якщо перетворення точку переводить в точку, то зворотне перетворення точку переводить в точку.
Розтягування (стиснення) відносно прямої є Афінний перетворення.
Нам залишилося показати, що стиснення і розтягнення прямі переводять в прямі. Нехай розтягнення здійснюється відносно прямої. Направимо уздовж неї вісь. Розглянемо будь-яку пряму. Можливі два випадки.
1) Якщо вона перетинається з, то проведемо через точку перетину вісь, перпендикулярну. Тоді рівняння прямої буде мати вигляд:
При розтягуванні щодо прямої (осі) з коефіцієнтом точка переходить в точку:
розтягнення щодо осі 'X'.
Точка прямий перейде в точку з координатами. А значить, координати нових точок будуть задовольняти рівняння
З через великий обсяг цей матеріал розміщений на декількох сторінках:
1 2 3 4 5