Опис презентації по окремим слайдів:
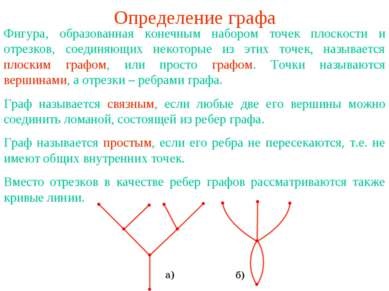
Визначення графа Фігура, утворена кінцевим набором точок площини і відрізків, що з'єднують деякі з цих точок, називається плоским графом, або просто графом. Точки називаються вершинами, а відрізки - ребрами графа. Граф називається зв'язковим, якщо будь-які дві його вершини можна з'єднати ламаною, що складається з ребер графа. Граф називається простим, якщо його ребра не перетинаються, тобто не мають спільних внутрішніх точок. Замість відрізків як ребер графів розглядаються також криві лінії.
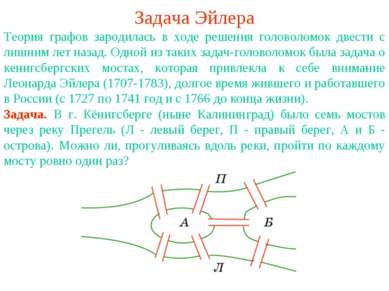
Завдання Ейлера Теорія графів зародилась в ході рішення головоломок двісті з гаком років тому. Однією з таких задач-головоломок була задача про кенігсберзькими мостах, яка привернула до себе увагу Леонарда Ейлера (1707-1783), який тривалий час жив і працював у Росії (з 1727 по 1741 рік і з 1766 до кінця життя). Завдання. В м Кенігсберзі (нині Калінінград) було сім мостів через річку Прегель (Л - лівий берег, П - правий берег, А і Б - острова). Чи можна, прогулюючись уздовж річки, пройти по кожному мосту рівно один раз?
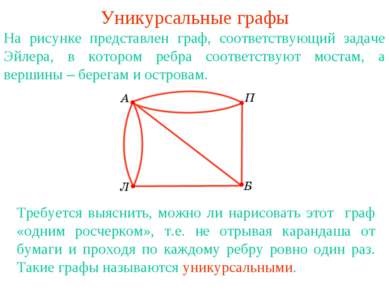
Унікурсальние графи На малюнку представлений граф, відповідний завданню Ейлера, в якому ребра відповідають мостам, а вершини - берегах і островах. Потрібно з'ясувати, чи можна намалювати цей граф «одним розчерком», тобто не відриваючи олівця від паперу і проходячи по кожному ребру рівно один раз. Такі графи називаються унікурсальнимі.

Теорема Індексом вершини графа називається число ребер, що сходяться в цій вершині (ребра, з початком і кінцем в даній вершині вважаються двічі). Теорема. Для унікурсального графа число вершин непарного індексу дорівнює нулю або двом. Доведення. Якщо граф унікурсален, то у нього є початок і кінець обходу. Решта вершини мають парний індекс, так як з кожним входом в таку вершину є і вихід. Якщо початок і кінець не збігаються, то вони є єдиними вершинами непарного індексу. У початку виходів на один більше, ніж входів, а у кінця входів на один більше, ніж виходів. Якщо початок збігається з кінцем, то вершин з непарним індексом немає. Вірно і зворотне: Якщо у зв'язкового графа число вершин непарного індексу дорівнює нулю або двом, то він є унікурсальним.

Рішення завдання Ейлера рішення задачі Ейлера. Знайдемо індекси вершин графа завдання Ейлера. Вершина А має індекс 5, Б - 3, П - 3 і Л - 3. Таким чином, ми маємо чотири вершини непарного індексу, і, отже, даний граф не є унікурсальним. Значить, не можна пройти по кожному з семи мостів тільки один раз.

Питання 1 Яка фігура називається графом? Відповідь: Графом називається фігура, утворена кінцевим набором точок площини і відрізків, що з'єднують деякі з цих точок.

Питання 2 Який граф називається унікурсальним? Відповідь: Граф називається унікурсальним, якщо його можна намалювати «одним розчерком», тобто не відриваючи олівця від паперу і проходячи по кожному ребру рівно один раз.

Питання 3 Що називається індексом вершини графа? Відповідь: Індексом вершини графа називається число ребер, що сходяться в цій вершині (ребра, з початком і кінцем в даній вершині вважаються двічі).

Питання 4 Що можна сказати про індекси вершин унікурсального графа? Відповідь: Для унікурсального графа число вершин непарного індексу дорівнює нулю або двом.
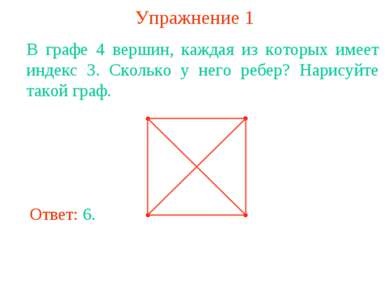
Вправа 1 В графі 4 вершин, кожна з яких має індекс 3. Скільки у нього ребер? Намалюйте такий граф.
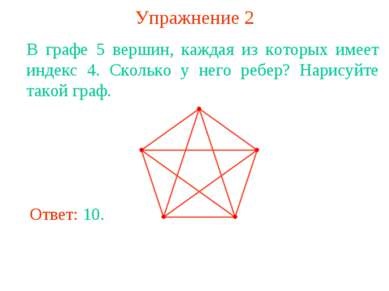
Вправа 2 У графі 5 вершин, кожна з яких має індекс 4. Скільки у нього ребер? Намалюйте такий граф.
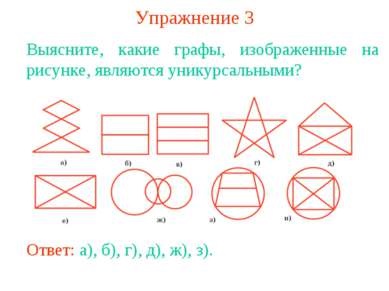
Вправа 3 З'ясуйте, які графи, зображені на малюнку, є унікурсальнимі? Відповідь: а), б), г), д), ж), з).

Вправа 4 Чи може граф мати: а) одну вершину непарного індексу; б) дві вершини непарного індексу; в) три вершини непарного індексу; г) чотири вершини непарного індексу? Відповідь: а), в) Ні; б), г) так.
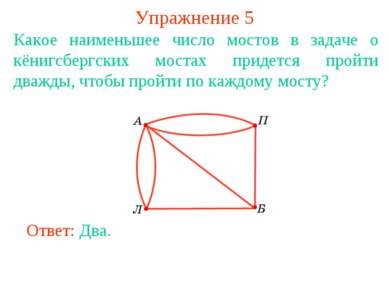
Вправа 5 Яке найменше число мостів в завданню про Кенігсбергськая мостах доведеться пройти двічі, щоб пройти по кожному мосту? Відповідь: Два.
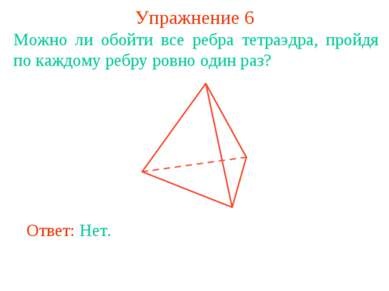
Вправа 6 Чи можна обійти всі ребра тетраедра, пройшовши по кожному ребру рівно один раз? Відповідь: Ні.
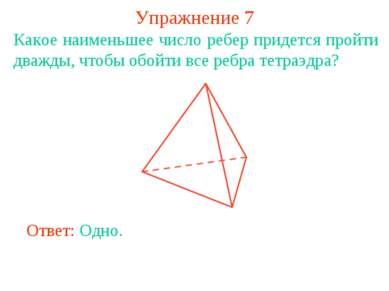
Вправа 7 Яке найменше число ребер доведеться пройти двічі, щоб обійти всі ребра тетраедра? Відповідь: Одне.

Вправа 8 Яке найменше число ребер доведеться пройти двічі, щоб обійти всі ребра тетраедра і повернутися у вихідну вершину? Відповідь: Два.
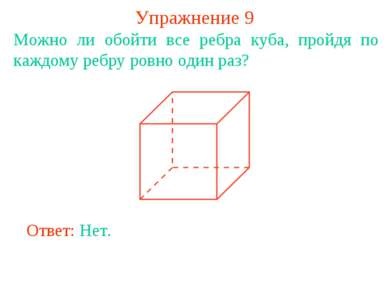
Вправа 9 Чи можна обійти всі ребра куба, пройшовши по кожному ребру рівно один раз? Відповідь: Ні.
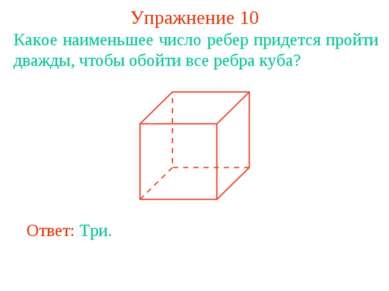
Вправа 10 Яке найменше число ребер доведеться пройти двічі, щоб обійти всі ребра куба? Відповідь: Три.
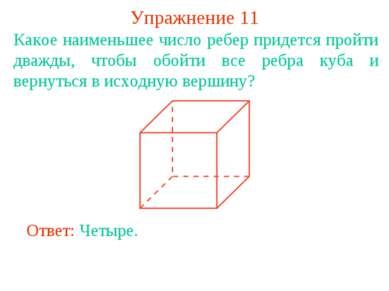
Вправа 11 Яке найменше число ребер доведеться пройти двічі, щоб обійти всі ребра куба і повернутися у вихідну вершину? Відповідь: Чотири.
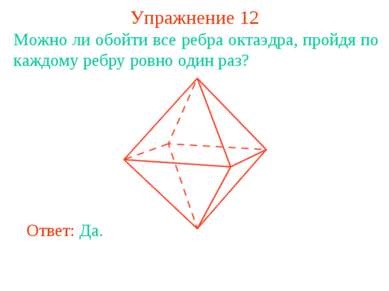
Вправа 12 Чи можна обійти всі ребра октаедра, пройшовши по кожному ребру рівно один раз? Відповідь: Так.

Вправа 13 Чи можна обійти всі ребра ікосаедра, пройшовши по кожному ребру рівно один раз? Відповідь: Ні.

Вправа 14 Яке найменше число ребер доведеться пройти двічі, щоб обійти всі ребра ікосаедра? Відповідь: П'ять.

Вправа 15 Яке найменше число ребер доведеться пройти двічі, щоб обійти всі ребра ікосаедра і повернутися у вихідну вершину? Відповідь: Шість.
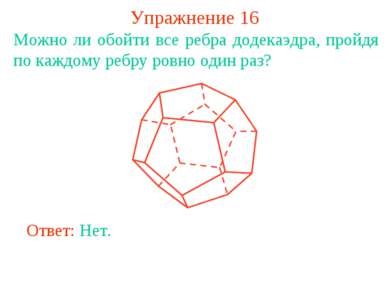
Вправа 16 Чи можна обійти всі ребра додекаедра, пройшовши по кожному ребру рівно один раз? Відповідь: Ні.
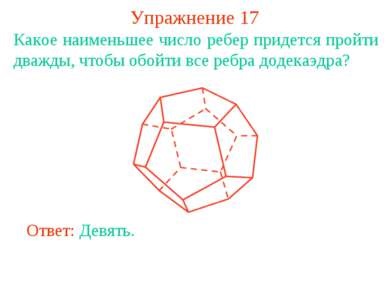
Вправа 17 Яке найменше число ребер доведеться пройти двічі, щоб обійти всі ребра додекаедра? Відповідь: Дев'ять.
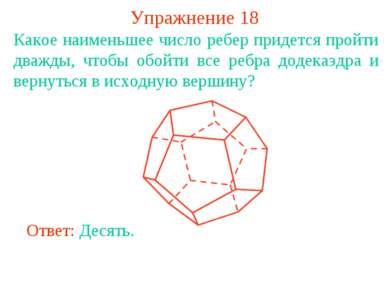
Вправа 18 Яке найменше число ребер доведеться пройти двічі, щоб обійти всі ребра додекаедра і повернутися у вихідну вершину? Відповідь: Десять.
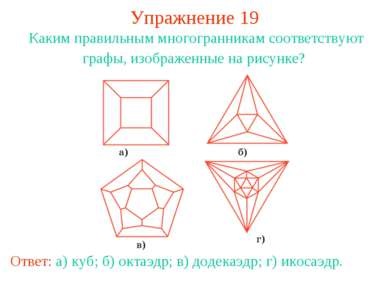
Вправа 19 Яким правильним многогранників відповідають графи, зображені на малюнку? Відповідь: а) куб; б) октаедр; в) додекаедр; г) ікосаедр.
Схожі презентації

Портфоліо моделі і фотографа

Визначення видів тварин і птахів околиць селища Хані, місця їх проживання в залежності від природно - кліматичних особливостей місцевості

Визначення змісту йоду в продуктах харчування

Визначення сили тертя ковзання

Кількісне визначення вітаміну С в продуктах харчування йодометричним методом

Визначення ролі собаки в історії людського суспільства і сприйняття її в різних етнокультурних традиціях

Графи. Ступінь вершини. Підрахунок числа ребер графа

Самовизначення учнів гімназії в майбутню професію
7311 7866 7998 9579 9630 9867 10685 11581
Презентації до уроку Геометрія

Синус, косинус, тангенс кута 9 клас

ознаки паралелограма

Симетрія - навколо нас

завдання вступних іспитів


Геометричні побудови за допомогою циркуля і лінійки


"Ймовірність"


багатогранники

осьова і центральна симетрія

Дивитися всі презентації з геометрії
32685 32738 32752 32898 32920 33141 33503 33504 33522 33751 33939 34145