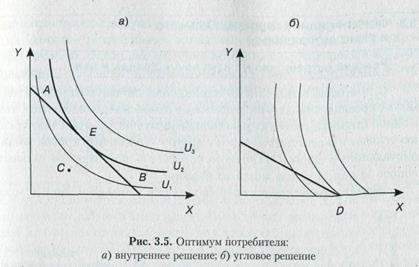
Для визначення оптимального споживчого вибору сов-якої точки на карті байдужості з бюджетним обмеженням споживача (рис. 3.5а).
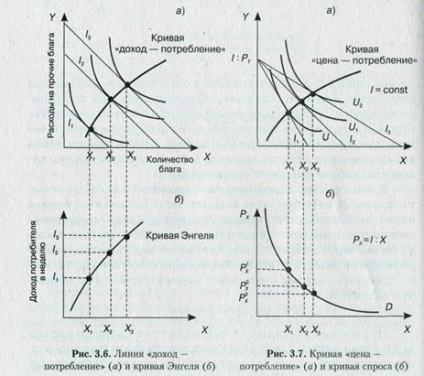
Оптимум досягається в точці Е, де бюджетна лінія стосується відповідної кривої байдужості U2i тобто має з нею тільки одну спільну точку. Дана крива буде, таким чином, єдність-ний для цієї точки.
Обгрунтувати оптимальність вибору в точці Е можна в такий спосіб. Очевидно, що корисність U3 недоступна споживачеві по бюд-жету. Точки, подібні точці С, що знаходяться всередині бюджетної обла-сті, не забезпечують споживачеві максимум доступною корисності, оскільки вони відповідають випадку, коли бюджет витрачений не повністю, і корисність може бути збільшена просто за рахунок додат-Передачі закупівель благ. Точки перетину кривих байдужості з бюд-
житній лінією А і В неоптимальні в сенсі невірної структури споживання, тому що занадто багато бюджетних коштів витрачено-но на товар з відносно низькою споживчою цінністю. При цьому завжди можна перерозподілити структуру витрат на по-споживання, замінивши, скажімо, товар У на товар X таким чином, щоб вивільнені кошти принесли велику додаткову корисність, а загальна корисність б збільшилася.
У точці дотику E досягається максимальний рівень полезнос-ти, доступний споживачеві по бюджету, коли бюджет витрачено повністю. Причому відносні переваги споживача рівні сформованим ціновим співвідношенням благ. Іншими словами, Накло-ни обох ліній збігаються (по властивості дотичних), тому соблю-дається рівність Px: Pty = MRSxy. Це відповідає еквімарясінально-му принципом - кожен рубль витрат приносить однакову предель-ву корисність:
На малюнку 3.56 показаний випадок, коли точка дотику знаходиться за межами позитивного квадранта, наприклад при яскраво виражений-ном перевагу одного блага щодо іншого. Тоді спожи-тель приходить до так званого кутового рішенням - його вибір сво-диться до повної відмови від покупки менш цінного блага (точка D), а весь бюджет витрачається на інше благо.