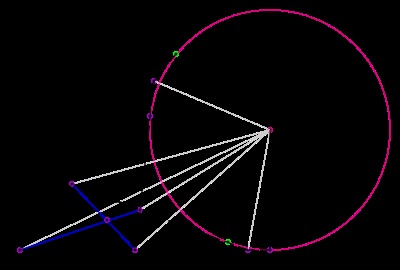
Внеопісанний чотирикутник ABCD і його вневпісанних кіл
Внеопісанний чотирикутник - це опуклий чотирикутник. продовження всіх чотирьох сторін якого є дотичними до кола (поза чотирикутника) [1]. Коло називається вневпісанних. Центр вневпісанних кіл лежить на перетині шести биссектрис. Це бісектриси двох внутрішніх кутів протилежних кутів чотирикутника, бісектриси зовнішніх кутів двох інших вершин, і бісектриси зовнішніх кутів в точках перетину продовжень протилежних сторін (дивіться малюнок праворуч, зазначені продовження сторін проведені пунктиром). Внеопісанний чотирикутник тісно пов'язаний з описаним чотирикутником (у якого чотири сторони стосуються окружності).
Дельтоіди є прикладом внеопісанних чотирикутників. Паралелограми (які включають квадрати. Ромби і прямокутники) можна вважати внеопісаннимі чотирикутника з нескінченним радіусом вневпісанних кіл, оскільки вони задовольняють властивостям, описаним нижче, але внеопісанная коло не може стосуватися обох пар продовжень сторін (з огляду на їх паралельності) [2]. Опуклі чотирикутники, довжини сторін яких утворюють арифметичну прогресію. завжди є внеопісаннимі, оскільки задовольняють умовам, описаним нижче для суміжних сторін.
Опуклий чотирикутник є внеопісанним тоді і тільки тоді. коли існує шість перетинаються в одній точці биссектрис. Це бісектриси двох внутрішніх кутів протилежних кутів чотирикутника, бісектриси зовнішніх кутів двох інших вершин і бісектриси зовнішніх кутів в точках перетину продовжень протилежних сторін [2].
З точки зору обчислень, більш корисно властивість, що опуклий чотирикутник зі сторонами a, b, c, d є внеопісанним тоді і тільки тоді, коли сума двох суміжних сторін дорівнює сумі двох інших сторін. Це можливо в двох випадках - або
Властивість доведено Якобом Штейнером в 1846 році [3]. У першому випадку вневпісанних кіл знаходиться з боку більшого з кутів при вершинах A або C. в той час як у другому випадку коло знаходиться з боку більшого з кутів при вершинах B або D. Тут боку чотирикутника ABCD мають довжини a = AB. b = BC. c = CD і d = DA. Комбінуючи два отриманих рівності, отримаємо, що абсолютні величини різниць протилежних сторін рівні [2],
Це рівність тісно пов'язане з теоремою Піто для описаних чотирикутників. по якій суми протилежних сторін рівні.
теорема Уркхарт
Якщо протилежні сторони опуклого чотирикутника ABCD перетинаються в точках E і F. то
Висновок зліва направо названий ім'ям Л. М. Уркхарт (1902-1966), хоча доведено задовго до нього Огастес де Морганом в 1841 році. Даніель Педо (Daniel Pedoe) назвав це твердження найелементарнішій теоремою геометрії Евкліда. оскільки в ній мова йде лише про прямі і відстанях [4]. Еквівалентність довів Моваффак Хаджу (Mowaffac Hajja) [4]. що зробило рівність справа іншим необхідною і достатньою умовою для того, щоб чотирикутник був внеопісанним.
Порівняння з описаним чотирикутником
Кілька показників описаних чотирикутників (лівий стовпчик таблиці) мають дуже схожого двійника для внеопісанного четирёхугоольніков (середній і правий стовпець таблиці), як можна бачити в таблиці нижче [2]. Так, опуклий чотирикутник має вписану або вневпісанних кіл близько відповідної вершини (залежить від стовпчика) тоді і тільки тоді, коли виконується будь-яка з п'яти умов.
Вневпісанних поза A або C
Вневпісанних поза B або D