Важливою характеристикою термодинамич-ської системи є її внутрішня енергіяU - енергія хаотичного (тепло-вого) руху мікрочастинок системи (молекул, атомів, електронів, ядер і т. Д.) І енергія взаємодії цих частинок. З цього визначення випливає, що до внутріш-ній енергії не відносяться кінетична енергія руху системи як цілого і потенційна енергія системи в зовнішніх полях.
Внутрішня енергія - однозначна функція термодинамічного стану системи, т. Е. В кожному стані система має цілком певною внутрішньою енергією (вона не залежить від того, як система прийшла в цей стан). це
означає, що при переході системи з одного стану в інший зміна внутрішньої енергії визначається тільки раз-ністю значень внутрішньої енергії цих станів і не залежить від шляху переходу. У § 1 було введено поняття числа ступенів свободи - числа незалежних змінних (координат), повністю визна-ділячи положення системи у просторі стве. У ряді завдань молекулу одноатомного газу (рис. 77, а) розглядають як мате-ріальну точку, якої приписують три
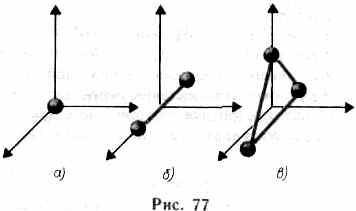
ступеня свободи поступального руху-ня. При цьому енергію обертального руху можна не враховувати (r-> 0, J = mr 2 ®0, tвр = Jw 2 / 2®0).
У класичній механіці молекула двоатомних газу в першому наближенні розглядається як сукупність двох матеріальних точок, жорстко пов'язаних недеформируемой зв'язком (рис. 77, б). Ця система крім трьох ступенів свободи по-поступального руху має ще два ступені свободи обертального руху. Обертання навколо третьої осі (осі, що проходить через обидва атома) позбавлене сенсу. Таким чином, двоатомний газ володіє п'ятьма ступенями свободи (i = 5). Трьохатомна (рис. 77,0) і багатоатомна нелінійні молекули мають шість степу-ній волі: три поступальних і три обертальних. Природно, що жорсткого зв'язку між атомами не існує. По-цьому для реальних молекул необхідно враховувати також ступеня свободи колеба-ного руху.
Незалежно від загального числа ступенів свободи молекул три ступені свободи завжди поступальні. Жодна з по-поступального ступенів свободи не має переваги перед іншими, тому на кожну з них припадає в середньому оди-наково енергія, рівна 1/3 значення У класичній статистичній фізиці виводиться закон Больцмана про рівномірний-ном розподілі енергії за ступенями свободи молекул: для статистичної системи, яка перебуває в стані термо-динамічної рівноваги, на кожну по-поступального і обертальну ступеня свободи доводиться в середньому кинетич-ська енергія, равнаяkT / 2 , а на кожну коливальну ступінь свободи - в середовищ-ньому енергія, равнаяkT. Коливальна ступінь «володіє» вдвічі більшою енер-гією тому, що на неї припадає не тільки кінетична енергія (як в слу-чаї поступального і обертального дви-жений), але і потенційна, причому середовищ-ня значення кінетичної і потенційної енергій однакові. Таким чином, середня енергія молекули де i - сума числа поступателен-них, числа обертальних і подвоєного числа коливальних ступенів свободи молекули: У класичній теорії розглядають молекули з жорсткою зв'язком між атома-ми; для них i збігається з числом ступенів свободи молекули. Так як в ідеальному газі взаємна потенційна енергія молекул дорівнює ну-лю (молекули між собою не взаємодій-обхідних), то внутрішня енергія, віднесений-ва до одного молю газу, буде дорівнює сумі кінетичних енергій NA молекул: Внутрішня енергія для довільної маси т газу де М - молярна маса, v - кількістю-ство речовини. Перший початок термодинаміки Q = U2 -U1 + A; при нескінченно малій зміні стану системи: де - нескінченно мале кількість теплоти, переданої системі, - робота, що здійснюються системою проти зовн. сил, dU - зміна її внутр. енергії.
Ур-ня (1) є визначенням величини dU. т. к. і - незалежно вимірювані величини. П. н. т. стверджує, що dU є повний диференціал деякої ф-ції U (величини і. взагалі кажучи, не є повними диференціалами). Т. о. будь-яка термодинамич. система має ф-цією стану - енергією U. залежить лише від параметрів, що визначають рівноважний стан системи, і не залежить від процесу, до-рим система була приведена в цей стан. Передане тепло Q і робота А залежать від шляху, по до-рому відбувається процес, т. К. Величини і не є повні диференціали.Схожі статті