Припустимо, що при складанні деякого проекту виокрем-лено 12 подій: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 і 24 пов'язую щие їх роботи: (0-1), (0-2), (0-3), (1-2), (1-4), (1-5), (2-3), (2-5), (2-7), (3 -6), (3-7), (3-10), (4-8), (5-8), (5-7), (6-10), (7-6), (7-8 ), (7-9), (7-10), (8-9), (9-11), (10-9), (10-11). Необхідно скласти і впорядкувати мережевий графік.
Як випливає з переліку робіт, вихідним подією мережевого графіка є подія 0 (йому не передують ніякі рабо-ти), а завершальним - подія 11 (за ним не слід ні одна робота). Вважаючи на мережевих графіках зміна часу зліва направо, помістимо подія 0 в ліву частину графіка, а подія 11 - в праву частину, розмістивши між ними проміжні со-буття в деякому порядку, відповідному їх номерами (рис. 13). Події зв'яжемо роботами-стрілками відповідно до переліку робіт.
Побудований мережевий графік задовольняє сформульованим вище правилам, що пред'являються до його побудови. Однак цей графік не повністю впорядкований.
Впорядкування мережевого графіка полягає в такому располо-жении подій і робіт, при якому для будь-якої роботи предшест-вующее їй подія розташоване лівіше і має менший номер в порівнянні з завершальним цю роботу подією. Іншими словами, в упорядкованому мережевому графіку всі роботи-стрілки направле-ни зліва направо: від подій з меншими номерами до подій з великими номерами.
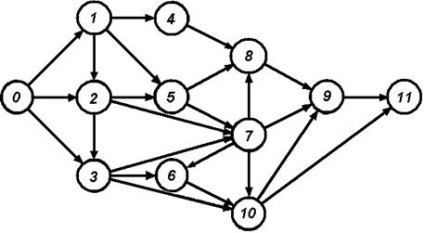
Мал. 13. Складений мережевий графік
Розіб'ємо умовно мережевий графік на декілька вертикальних шарів (обводимо їх пунктирними лініями і позначаємо римски-ми цифрами).
Помістивши в I шарі початкова подія 0 (рис. 14), подумки викреслимо з графіка (див. Рис. 13) ця подія і усі, хто виходив з нього роботи-стрілки. Тоді без вхідних стрілок залишиться подія 1, який утворює II шар. Викресливши подумки подія 1 і усі, хто виходив з нього роботи, побачимо, що без вхідних стрілок залишаються події 4 і 2, які утворюють III шар. Продовжуючи зазначену процедуру викреслювання, отримаємо IV шар з подіями 5 і 3, V шар - з подією 7, VI шар - з подіями 8 і 6, VII шар - з подією 10, VIII шар - з подією 9 і, нарешті, IX шар - з подією 11.
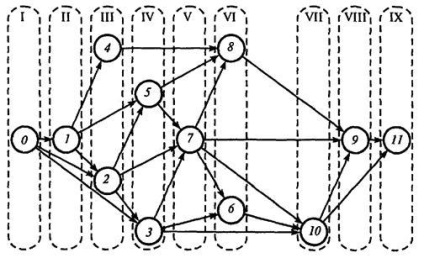
Мал. 14. Мережевий графік, розбитий на кілька вертикальних шарів
Тепер бачимо, що первісна нумерація подій не з-усім правильна: так, подія 6 лежить в VI шарі і має номер, менший, ніж подія 7 з попереднього шару. Те ж можна ска-мовити про події 9 і 10.
Змінимо нумерацію подій відповідно до їх расположе-ням на графіку (див. Рис. 14) і отримаємо впорядкований сеті-вої графік (рис. 15), в якому над стрілками вказана продов-жительность відповідних робіт (в днях). (Порядок нумерації подій, розташованих в одному вертикаль-ном шарі, принципового значення не має, так що нумерація одно-го і того ж мережевого графіка може бути неоднозначною.)
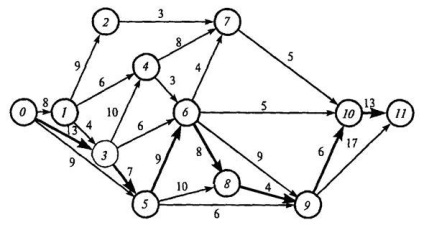
Мал. 15. Упорядкований мережевий графік
Тривалості очікуваного часу виконання робі-бот відображаються на мережевому графіку над роботами-стрілками (див. Рис. 15). На їх основі проводиться подальший розрахунок параметрів мережного графіка.
Одне з найважливіших понять мережевого графіка - поняття шляху. Шлях - будь-яка послідовність робіт, в якій кінцева подію-тя кожної роботи збігається з початковим подією наступної за нею роботи. Серед різних шляхів мережевого графіка найбільший інтерес представляє повний шлях L - будь-який шлях, початок якого збігається з вихідним подією мережі, а кінець - із завершальним.
Найбільш тривалий повний шлях в мережевому графіку на-ни опиняються критичним. Критичними називаються також роботи і події, розташовані на цьому шляху.
Наприклад, для розглянутого мережевого графіка (див. Рис. 15) повними шляхами будуть:
- шлях 0® 5® 8® 9® 11 тривалістю 9 + 10 + 4 + 17 = 40 дн .;
Можна переконатися в тому, що останній шлях має наиболь-шую тривалість (не тільки серед наведених чотирьох повних шляхів, а й серед усіх повних шляхів, яких в дан-ном випадку налічується 64), тому він і є критичним. Тривалість критичного шляху становить 60 днів, тобто для проведення комплексу робіт необхідно 60 днів. Швидше комплекс виконати не можна, так як для досягнення завершального події критичний шлях потрібно пройти обов'язково.
Дійсно, для досягнення події 11 треба виконати роботу (10-11), тобто досягти події 10; для досягнення події 10 треба провести роботу (9-10), тобто досягти події 9; для дос-тижения події 9 треба провести роботу (8-9), тобто досягти з-буття 8, і т.д.
Визначивши критичний шлях, ми тим самим встановили критичні події мережі 0, 3, 5, 6, 8, 9, 10 і 11 та критичні роботи (0-3), (3-5), (5-6), ( 6-8), (8-9), (9-10), (10-11).
Критичний шлях має особливе значення в системі СПУ, так як роботи цього шляху визначають загальний цикл завершення всього комплексу робіт, що плануються за допомогою мережевого графіка. І для скорочення тривалості проекту необхідно в пер-шу чергу скорочувати тривалість робіт, що лежать на критичному шляху.