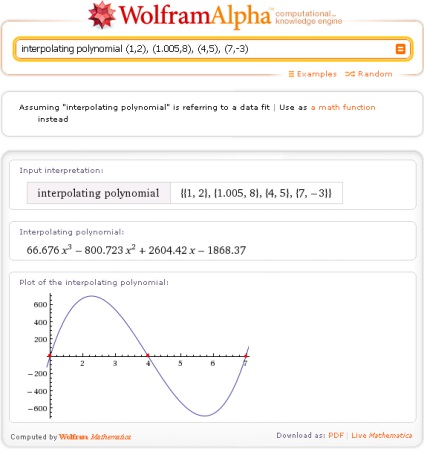
Інтерполяція - різновид апроксимації. Однак, на відміну від апроксимації за методом найменших квадратів, яка дає рівняння функції з графіком, який проходить на мінімальній відстані від кожної з даних точок, завдання інтерполяції полягає в тому, щоб знайти рівняння функції, графік якої проходить точно через всі задані точки.
Існують різні види інтерполяції. Wolfram | Alpha використовує поліноміальних інтерполяцію, і виконує її за запитом interpolating polynomial
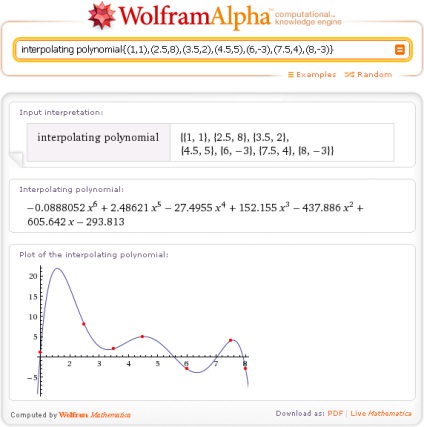
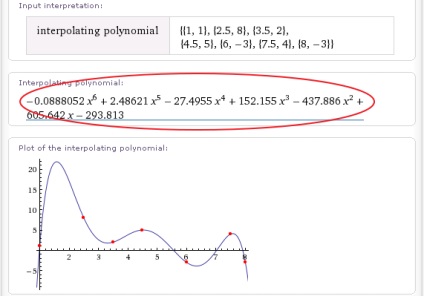
У відповідь Wolfram | Alpha видасть (б) набір відомостей про це вираженні, як якщо б ви ввели його вручну:
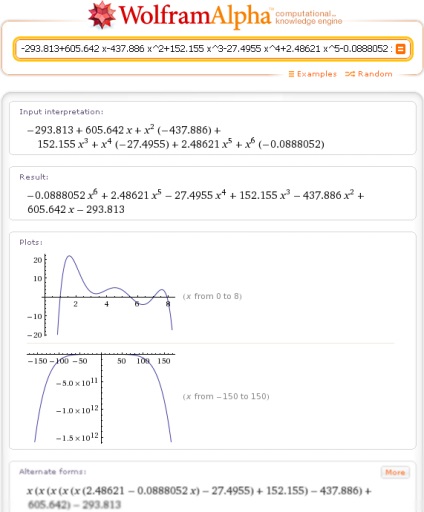
Нарешті (в), щоб обчислити значення інтерполяційного полінома в заданій точці (x = 4), потрібно просто вказати у вікні запиту Wolfram | Alpha, після введеного полінома через кому, значення аргументу, щоб вийшло таке:

Апроксимація по тому ж самому набору точок, коли невідомий ні тип ні порядок моделі апроксимації, дає наступне:
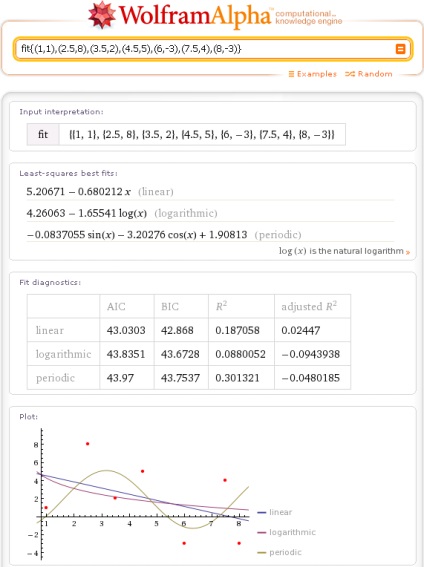
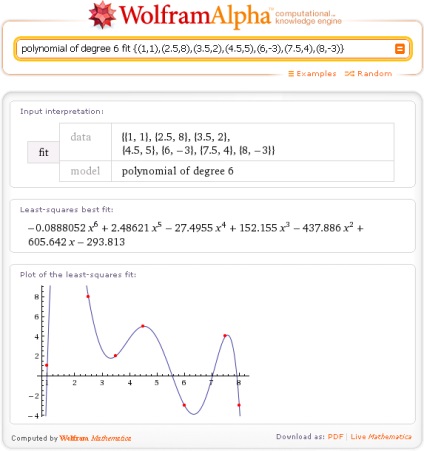
Можна отримати результат апроксимації, що співпадає з результатом полиномиальной інтерполяції. Для цього потрібно вибрати поліноміальних модель і вказати її порядок на 1 менше, ніж кількість даних точок:
Для виконання інтерполяції важливо, щоб абсциси заданих точок не збігалися. Наприклад, ось такий запит (це НЕПРАВИЛЬНО!)
де перша і друга точка мають однакову абсциссу, дає результат на перший погляд правдоподібний, але абсолютно неправильний:
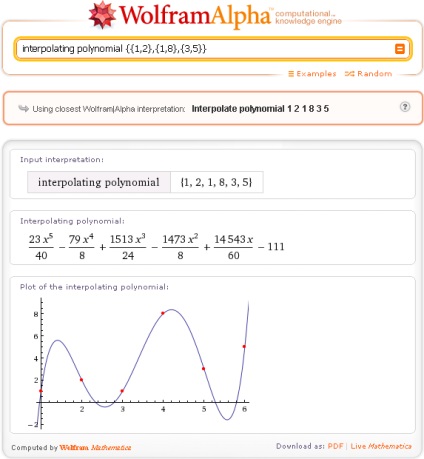
Тут, як бачите, Wolfram | Alpha інтерпретує координати 3-х даних точок, як послідовність з 6-ти чисел - значень функції, а в якості абсцис використовує номера членів цієї послідовності.
Якщо ж абсциси всіх точок хоч трохи, але відрізняються, то отримаємо абсолютно вірний результат (це ПРАВИЛЬНО!):