Завдання сподобалася, тому що проста, але не заяложена (я не зустрічав схожих).
План вирішення такого:
Повинні з'являтися відразу. Для незареєстрованих користувачів використовується кешування на 1 годину, для зареєстрованих воно автоматично відключається. Але ще є кешування з боку браузера.
Величезне спасибі! Обов'язково викладу рішення. -)
2) якщо T менше часу стрибка (що, ймовірно, мається на увазі), то найлегше вирішувати так:
інакше питання сенсу не має.
4) записати кінематичні рівняння руху на ці осі (не забути про проекції g. Що вони не нульові),
незрозуміло, навіщо складати кінематичні рівняння руху, якщо ми висловлюємо швидкість, пов'язуючи горизонтальну і вертикальну складові швидкості через час t в обраній СК на Сонце.
5) з кінематичного рівняння знайти швидкість в потрібний момент Т в проекції на вісь, перпендикулярну напрямку на сонці,
чи не буде це вертикальна складова швидкості?
2) має. Тоді швидкість 0. Повне рішення повинно задавати швидкість як функцію T. якщо T менше часу польоту і швидкість дорівнює 0. Якщо більше.
4) мається на увазі одне рівняння для швидкості.
5) чи не буде це вертикальна складова швидкості?
Якщо вісь на сонці OY. а їй перпендикулярна OX. то це буде проекція на вісь OX. Т.к вісь OX не вертикально, то це не буде вертикальна складова.
І ще: в плані вирішення помилка у мене: потрібно було написати не 1 / cos φ. а 1 / sin φ.
Запишемо рівняння зміни координати уздовж осі X.
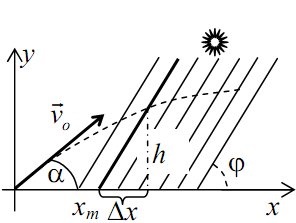
Координата кінця тіні буде визначатися виразом:
xm = x - δx = vo t cos α - h / tg φ.
де h - висота підйому коника в момент часу t.
h = vo t sin α - gt 2/2.
Зробивши заміну в рівняння координати тіні:
xm = (vo cos α - vo sin α / tg φ) × t + gt 2 / (2tg φ).
Продифференцировав рівняння координати за часом, знайдемо закон зміни швидкості тіні коника від часу: