У початковий момент руху швидкість циліндра дорівнює нулю і його повна механічна енергія дорівнює потенційної. При переході на горизонтальну площину повна механічна енергія циліндра дорівнює сумі кінетичної енергії і потенційної енергії циліндра. Згідно із законом збереження повної механічної енергії виходить:
Потенційна енергія циліндра визначається положенням центру мас циліндра над горизонтальною площиною. Тому:. де g - прискорення вільного падіння.
Як відомо, кочення циліндра по плоскій поверхні можна розглядати як поворот з кутовий швидкістю # 969; навколо миттєвої осі обертання, що проходить по лінії зіткнення циліндричної поверхні і площини. На малюнку миттєва вісь обертання проходить через точку М перпендикулярно площині малюнка. Отже, кінетична енергія визначається виразом
де I - момент інерції циліндра відносно миттєвої осі обертання. З відомого вислову для моменту інерції циліндра відносно осі симетрії і теореми Штейнера виходить:
Вираз (1) з урахуванням формул (2) і (3) набуває вигляду
З рівняння (4) для кутової швидкості # 969; слід:
Момент імпульсу L при переході циліндра на горизонтальну площину спрямований уздовж миттєвої осі обертання, як показано на малюнку. Модуль моменту імпульсу
відповідь: # 969; = 72 рад / с; L = 2,7 (кг × м²) / с.
12. Два кулі, один масою m1 = 2,0 кг, другий m2 = 3,0 кг, на горизонтальній площині рухаються назустріч у взаємно напрямках і стикаються абсолютно непружно. Знайти після зіткнення швидкість куль. напрямок швидкості і частина механічної енергії куль, що перейшла у внутрішню енергію куль. До зіткнення швидкість першої кулі = 5,0 м / с, другого = 3,0 м / с.
Рішення
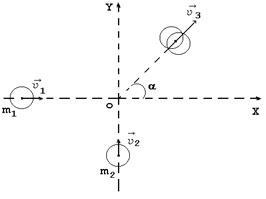
На горизонтальній площині введемо систему координат XOY. як показано на рис. 1. Зіткнення куль відбувається на початку системи координат. Зіткнення абсолютно непружні, тому кулі "злипаються" і рухаються разом зі швидкістю. як показано на рис. 1. Зовнішня сила (сила тяжіння), що діє на кулі, перпендикулярна до горизонтальної площини і, отже, виконується закон збереження імпульсу
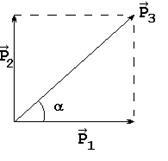
де - імпульс першої кулі до зіткнення; - імпульс другого кулі до зіткнення; - імпульс куль після зіткнення. З характеру руху куль і закону збереження імпульсу випливає, що напрямок векторів повинні відповідати рис. 2, а модулі векторів пов'язані співвідношенням або
З рівняння (2) для швидкості отримуємо:
кут # 945 ;, що характеризує напрямок швидкості. може бути знайдений з рис. 2 за формулою:
При абсолютно непружного зіткненні механічна енергія тіл зменшується на величину # 916; W. перейшла у внутрішню енергію куль. Рух відбувається на горизонтальній площині, тому механічна енергія системи обумовлена кінетичної енергією куль. Остаточно для величини # 916; W слід
Відповідь: = 2,7 м / с; # 945; = 42º; # 916; W = 20 Дж.
13. На лаві Жуковського обертається з частотою n1 = 1,0 об / с людина, що тримає в центрі горизонтально розташований металевий стрижень масою m = 5,0 кг і довжиною l = 1,5 м. Визначити частоту обертання людини n2 і досконалу роботу A . якщо він поверне стрижень у вертикальне положення. Момент інерції людини і лави I0 = 5,0 кг # 8729; м².
Рішення Обертання людини зі стрижнем відбувається навколо вертикальної осі, момент зовнішніх сил щодо якої дорівнює нулю. Тому величина моменту імпульсу L щодо вертикальної осі залишається незмінною при повороті стрижня, т. Е.. або (1)
де I1 і # 969; 1 - момент інерції і кутова швидкість людини зі стрижнем, розташованим горизонтально; I2 і # 969; 2 - момент інерції і кутова швидкість людини зі стрижнем, розташованим вертикально. Кутова швидкість # 969; і число оборотів в одиницю часу пов'язані співвідношенням
Момент інерції стержня Ic щодо осі, перпендикулярної до стрижня і проходить через його центр мас,. Тому
При повороті стержня в вертикальне положення його момент інерції стає рівним нулю. Отже, (4) Підставляючи співвідношення (2) - (4) в формулу (1), отримаємо:. Звідси для величини n2 слід:
Робота A. досконала людиною при повороті стрижня, дорівнює зміні кінетичної енергії. Тому
ЗАВДАННЯ ДЛЯ САМОСТІЙНОГО РОЗВ'ЯЗАННЯ
1.44. Платформа у вигляді диска обертається по інерції навколо вертикальної осі з частотою n1 = 14 хв -1. На краю платформи стоїть людина. Коли людина перейшла в центр платформи, частота зросла до n2 = 25 хв -1. Маса людини m = 70 кг. Визначити масу платформи. Момент інерції людини розраховувати як для матеріальної точки.
1.45. Людина масою m0 = 60 кг знаходиться на нерухомій платформі масою m = 100 кг. З якою частотою n буде обертатися платформа, якщо людина буде рухатися по колу радіусом r = 5,0 м навколо осі обертання? Швидкість руху людини щодо платформи u0 = 4,0 км / год. Радіус платформи R = 10 м. Вважати платформу однорідним диском, а людину - точковою масою.
1.46. Куля скочується з похилої площини висотою h = 90 см. Яку лінійну швидкість матиме куля в той момент, коли він скотиться з похилій площині? Момент інерції кулі J = 0,40 m × R 2.
1.47. Два кулі рухаються назустріч один одному уздовж осі Х. Маса першої кулі m1 = 0,20 кг, маса другого кулі m2 = 0,30 кг. До зіткнення проекції швидкостей куль на вісь = 1,0 м / с, = -1,0 м / с. Знайти проекції швидкостей куль і після центрального абсолютного пружного зіткнення.
(= -1,4 м / c; = 0,60 м / c)
1.48. Тонкий однорідний стрижень довжиною L може обертатися навколо горизонтальної осі, що проходить через кінець стержня перпендикулярно йому. Стрижень відхилили на 90 ° від положення рівноваги і відпустили. Визначити швидкість u нижнього кінця стрижня в момент проходження рівноваги.
1.49. Тонкий однорідний стрижень довжиною l і масою m може вільно обертатися навколо горизонтальної осі, що проходить через один з його кінців. Стрижень встановлюють горизонтально і відпускають. Нехтуючи тертям, визначити кутову швидкість стержня в момент проходження ним положення рівноваги. Побудувати графік залежності кутового прискорення стержня від кута між стрижнем і горизонтом.
1.50. Суцільний однорідний шар скочується по похилій площині довжиною 5,0 м. Кут нахилу площини до горизонту a = 30 °. Визначити швидкість кулі в кінці похилій площині, час руху кулі до горизонтальної поверхні і якісно побудувати залежність кінетичної енергії кулі як функцію часу. Втратами енергії знехтувати. Момент інерції кулі відносно осі, що проходить через центр мас, J0 = mR 2.
(U = 5,9 м / с; t = 1,7 c)
1.51. Суцільний циліндр котиться по горизонтальній поверхні протягом часу t = 3,0 c і зупиняється, пройшовши відстань 9,0 м. Визначити коефіцієнт тертя, вважаючи його постійним. Побудувати якісно залежність кінетичної енергії тіла як функцію часу руху.
1.52. Вал масою m = 50 кг і радіусом R = 5,0 см обертався з частотою n = 10 об / с. До його циліндричної поверхні притиснули гальмівну колодку з силою F = 30 Н, і через 8,0 с після початку гальмування вал зупинився. Визначити коефіцієнт тертя, вважаючи його постійним. Побудувати графік залежності кутової швидкості і кутового прискорення вала як функцію часу на інтервалі гальмування.
1.53. Куля і суцільний диск мають однакові маси і котяться без ковзання по горизонтальній поверхні з однаковими постійними швидкостями. Кінетична енергія кулі W1 = 70 Дж. Визначити кінетичну енергію диска W2. Знайти відношення проекцій моменту імпульсу тел Lz1 / Lz2 на миттєву вісь обертання, якщо R1 / R2 = 0,7.
1.54. Тіло масою М підвішено на нитці довжиною l. У тіло потрапляє куля масою m і застряє в ньому, нитка після цього відхиляється на кут a. Знайти швидкість кулі. Вважати, що вся маса тіла М зосереджена на відстані l від точки підвісу.
1.55. Скільки часу буде скочуватися циліндр з похилій площині довжиною l = 2,0 м і висотою h = 0,10 м, якщо вважати, що прослизання немає? Якісно побудуйте залежність кінетичної Wk і потенційної Wp енергії циліндра як функцію часу.
1.56. Два кулі масами m1 = 10 кг і m2 = 15 кг підвішені на нитках довжиною l = 2,0 м так, що кулі стикаються між собою. Менший куля був відхилений на кут j = 60 ° і відпущений. Визначити висоту, на яку піднімуться обидві кулі після удару. Удар куль вважати непружним.
1.57. У циліндр масою m1 = 3,0 кг і радіусом R = 10 см, що спочивають на площині, потрапляє куля масою m2 = 9,0 г, що летить зі швидкістю u0 = 60 м / с. Куля летить паралельно площині на висоті h = 0,12 м від неї і перпендикулярно твірної циліндра. Вважаючи удар абсолютно непружним, знайдіть лінійну швидкість осі циліндра, кутову швидкість циліндра. Проскальзиваніем циліндра знехтувати.
1.58. Тіла з масами m1 і m2 пов'язані невагомою і нерастяжимой ниткою, яка перекинута через блок масою m. встановлений на краю стола. Тіло m1 знаходиться на поверхні столу в закріпленому стані. Тіло m2 вільно висить. У момент часу t = 0 тіло m1 звільнили, і вся система прийшла в рух. Вважаючи коефіцієнт тертя між столом і тілом m1 рівним m, нехтуючи ковзанням нитки по блоку і тертям в осі блоку, знайти роботу сил тертя за перші t секунд після початку руху. Блок вважати однорідним диском.
1.59. Сталева кулька масою m = 8 г, що летить горизонтально зі швидкістю 600 м / с, потрапляє в брусок масою M = 4m. прикріплений до стінки пружиною з жорсткістю k = 24 кН / м. Вважаючи, що траєкторія кульки перпендикулярна поверхні бруска і збігається з віссю пружини, визначити величину максимального стиснення пружини, якщо наголос було:
1) абсолютно непружним; 2) абсолютно пружним.
Записати закон зміни деформації пружини як функцію від часу для випадків 1 і 2.
1.60. Поршень, закріплений на пружині жорсткістю k = 10 кН / м, після застрявання в ньому горизонтально яка летіла зі швидкістю u = 520 м / с кулі масою 20 г змістився на х = 8 см. Визначити масу поршня М. якщо сила тертя його об стінки циліндра становить 900 Н.
1.61. Нитка з підвішеним на ній вантажем відхилили на кут a і відпустили. На який кут b відхилиться нитка з вантажем, якщо при своєму русі буде затримана штифтом, поставленим по вертикалі посередині нитки? Побудувати якісну залежність швидкості вантажу від часу, вважаючи, що втрати енергії в системі не відбувається.
1.62. Хокейна шайба, маючи початкову швидкість u = 5,0 м / с, проходить до удару об борт майданчика шлях S = 10 м. Коефіцієнт тертя шайби об лід 0,10. Вважаючи удар об борт абсолютно пружним і нехтуючи опором повітря, визначити, який шлях пройде шайба після удару. Побудувати графік залежності ux = f (x), вважаючи позитивний напрямок осі ОХ до борту.
1.63. Людина стоїть на нерухомій візку і кидає горизонтально камінь масою m1 = 2,0 кг зі швидкістю u = 8,0 м / с. Визначити, яку роботу А робить при кидку людина, якщо маса візка з людиною m2 = 140 кг. Побудуйте графік залежності роботи A = f (m2), якщо m2 - величина змінна.
1.64. Гімнаст "крутить сонце" на перекладині. Вважаючи, що вся маса гімнаста m зосереджена в його центрі мас і швидкість гімнаста у верхній точці дорівнює нулю, визначити силу, що діє на руки гімнаста в нижчій точці. Побудувати графік залежності вертикальної складової швидкості гімнаста від часу uy = f (t). За початок відліку прийняти верхнє положення гімнаста. Тертям знехтувати.