Загасанням коливань називають зменшення амплітуди коливань з плином часу, обумовлене втратою енергії коливальної системою (наприклад, перетворення енергії коливань в теплоту внаслідок тертя в механічних системах). Загасання порушує періодичність коливань, тому вони вже не є періодичним процесом. Якщо загасання мало, то можна умовно користуватися поняттям періоду коливань - Т (на малюнку 7.6 А0 - початкова амплітуда коливань).
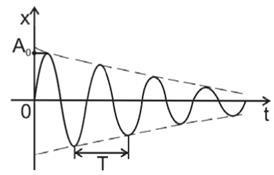
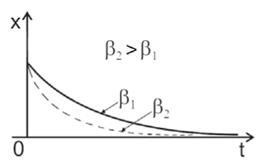
Малюнок 7.6 - Характеристики затухаючих коливань
Затухаючі механічні коливання пружинного маятника відбуваються під дією двох сил: сили пружності і сили опору:
де r - коефіцієнт опору.
Скориставшись рівнянням другого закону Ньютона, можна отримати:
Розділимо останнє рівняння на m і введемо позначення або
де # 946; коефіцієнт загасання, тоді рівняння прийме вид
Цей вираз і є диференціальне рівняння затухаючих коливань. Рішенням цього рівняння є
Звідси випливає експонентний характер згасаючих коливань, тобто амплітуда коливань зменшується за експоненціальним законом (рисунок 7.6):
Відносне зменшення амплітуди коливань за період характеризується декрементом загасання, рівним
або логарифмічним декрементом загасання:
коефіцієнт загасання # 946; обернено пропорційний часу # 964; протягом якого амплітуда коливань зменшується в e раз:
Частота згасаючих коливань завжди менше частоти власних коливань і може бути знайдена з виразу
де # 969; 0 частота власних коливань системи.
Відповідно період згасаючих коливань дорівнює:
Зі збільшенням тертя період коливань зростає, а при період.
Для отримання незатухаючих коливань необхідно вплив додаткової змінної зовнішньої сили, яка підштовхувала б матеріальну точку то в одну, то в іншу сторону і робота якої безперервно б восполняла спад енергії, що витрачається на подолання тертя. Така змінна сила називається винуждающейFвин. а що виникають під її дією незгасаючі коливання - вимушеними.
Якщо змушує сила змінюється в відповідністю з виразом, то рівняння вимушених коливань набуде вигляду
де # 969; циклічна частота змушує сили.
Це диференціальне рівняння вимушених коливань. Рі-ня його може бути записано у вигляді
Рівняння описує гармонійнеколивання, що відбувається з частотою, рівній частоті змушує сили, що відрізняється по фазі на # 966; щодо коливань сили.
Амплітуда вимушеного коливання:
Різниця фаз між коливаннями сили і системи знаходиться з ви-ражения
Графік вимушених коливань наведено на малюнку 7.7.
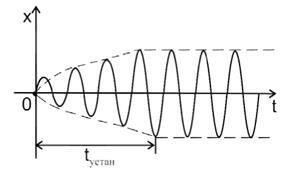
Малюнок 7.7 - Вимушені коливання
При вимушених коливаннях може спостерігатися таке явище, як резонанс. Резонанс це різке зростання амплітуди коливань системи.
Визначимо умову, за якої настає резонанс, для цього рас-дивимося рівняння (7.30). Знайдемо умову, за якої амплітуда при-нимает максимальне значення.
З математики відомо, що екстремум функції буде, коли про-похідних дорівнює нулю, тобто
Після перетворення отримуємо
Отже - резонансна частота.
У найпростішому випадку резонанс настає, коли зовнішня періоді-чна сила F змінюється з частотою # 969 ;. рівній частоті власних колеба-ний системи # 969; = # 969; 0.
Процес поширення коливань у суцільному середовищі, періодичний у часі і просторі, називається хвильовим процесом або хвилею.
При поширенні хвилі частинки середовища не рухаються разом з хвилею, а коливаються біля своїх положень рівноваги. Разом з хвилею від частинки до частинки середовища передається лише стан коливального руху і його енергія. Тому основною властивістю хвиль, незалежно від їх природи, є перенесення енергії без перенесення речовини.
Виділяють такі типи хвиль:
Пружними (або механічними) хвилями називаються механічні обурення, що поширюються в пружному середовищі. У будь-який пружною хвилі одночасно існують два види руху: коливання частинок середовища і поширення обурення.
Хвиля, в якій коливання частинок середовища і поширення хвилі відбуваються в одному напрямку, називається поздовжньої. а хвиля, в якій частинки середовища коливаються перпендикулярно напрямку поширення хвилі, називається поперечною.
Поздовжні хвилі можуть поширюватися в середовищах, в яких виникають пружні сили при деформаціях стиску і розтягування, тобто твердих, рідких і газоподібних тілах. Поперечні хвилі можуть поширюватися в середовищі, в якій виникають пружні сили при деформації зсуву, тобто в твердих тілах. Таким чином, в рідинах і газах виникають лише подовжні хвилі, а у твердих тілах - як подовжні, так і поперечні.
Пружна хвиля називається синусоїдальною (або гармонічною), якщо відповідні їй коливання частинок середовища є гармонічними.
Відстань між найближчими частинками, що коливаються в однаковій фазі, називається довжиною хвилі # 955; .
Довжина хвилі дорівнює відстані, на яке поширюється хвиля за час, що дорівнює періоду коливань:
де - швидкість поширення хвилі.
Так як (де # 957; частота коливання), то
Геометричне місце точок, до яких доходять коливання до моменту часу t. називається хвильовим фронтом. Геометричне місце точок, хто вагається в однаковій фазі, називається хвильовою поверхнею.
Біжать хвилями називають хвилі, які переносять в просторі енергію. Для виведення рівняння біжучої хвилі - залежно зміщення коливної точки від координати і часу - розглянемо плоску синусоїдальну хвилю, що поширюється уздовж осі х.
Нехай в якійсь точці середовища Про розташоване джерело коливань:
В деякій точці В. знаходиться на відстані х від джерела,
коливання будуть відставати за часом від коливань в точці О. так як для проходження хвилею відстані х потрібен час. де - швидкість поширення хвилі.
Рівняння коливань в точці В матиме вигляд
Так як а то
Після підстановки рівняння хвилі, що біжить уздовж осі х:
В теорії хвиль користуються поняттям хвильового вектора:
Абсолютне значення хвильового вектора дорівнює числу довжин хвиль на відрізку 2π. Хвильовий вектор орієнтований в просторі в напрямку поширення хвилі.
У загальному випадку рівняння біжучої хвилі, що розповсюджується в просторі вздовж осі х. має вигляд
де хвильове число, а фазова швидкість, або швидкість поширення хвилі
Фазова швидкість залежить від частоти
Хвильове рівняння в цьому випадку має вигляд
Цьому рівнянню задовольняють плоска і сферична хвилі.