Мал. 3. Граф кенігсберзькими мостів
Кілька модифікуємо завдання. Кожну з розглянутих місцевостей, розділених річкою, позначимо точкою, а що з'єднують їх мости - відрізком лінії (не обов'язково прямий). Тоді замість плану будемо працювати просто з якоїсь фігурою, складеної з відрізків кривих і прямих. Такі фігури в сучасній математиці називаються графами, відрізки - ребрами, а точки, які з'єднують ребра - вершинами. Тоді вихідна задача еквівалентна наступній: чи можна накреслити даний граф, не відриваючи олівця від паперу, тобто таким чином, щоб кожне його ребро пройти рівно один раз.
Такі графи, які можна накреслити, не відриваючи олівця від паперу, називаються унікурсальнимі (від латинського unus cursus - один шлях), або ейлеровимі. Отже, завдання ставиться таким чином: за яких умов граф унікурсален? Ясно, що унікурсальний граф не перестане бути унікурсальним, якщо змінити довжину або форму його ребер, а також змінити розташування вершин - аби не змінювалося з'єднання вершин ребрами (в тому сенсі, що якщо дві вершини з'єднані, вони повинні залишатися з'єднаними, а якщо роз'єднані - то роз'єднаними).
Мал. 4. Топологічно еквівалентні графи
Якщо граф унікурсален, то і топологічно еквівалентний йому граф теж буде унікурсальним. Унікурсальность, таким чином, є топологічним властивістю графа.
По-перше, треба відрізняти зв'язкові графи від незв'язних. Зв'язковими називаються такі фігури, що будь-які дві точки можна з'єднати якимось шляхом, що належить цій фігурі. Наприклад, велика частина букв російського алфавіту зв'язні, але ось буква И - немає: неможливо перейти з її лівої половинки на праве по точкам, що належить цій букві. Можливості підключення - це топологічний властивість: воно не змінюється при перетвореннях фігури без розривів і склеювань. Зрозуміло, що якщо граф унікурсален, то він зобов'язаний бути зв'язковим.
По-друге, розглянемо вершини графа. Будемо називати індексом вершини число ребер, що зустрічаються в цій вершині. Тепер запитаємо себе: чому можуть дорівнювати індекси вершин унікурсального графа.
Тут може бути два випадки: лінія, викреслюють граф, може починатися і закінчуватися в одній і тій же точці (назвемо її «замкнутий шлях»), а може в різних (назвемо її «незамкнений шлях»). Спробуйте самі намалювати такі лінії - з якими хочете самоперетинів - подвійними, потрійними і т. Д. (Для наочності краще, щоб ребер було не більше 15).
Неважко бачити, що в замкнутому шляху все вершини мають парний індекс, а в незамкнутому - рівно дві мають непарний (це початок і кінець шляху). Справа в тому, що, якщо вершина не є початковою або кінцевою, то, прийшовши до неї, треба потім з неї вийти - таким чином, скільки ребер входять в неї, стільки ж виходять з неї, а всього число вхідних і вихідних ребер буде парних . Якщо початкова вершина збігається з кінцевою, то її індекс також четен: скільки ребер з неї вийшло, стільки ж і увійшло. А якщо початкова точка не збігається з кінцевою, то їх індекси непарні: з початкової точки потрібно один раз вийти, а потім, якщо в неї і повернемося, то вийти знову, якщо ще раз повернемося - знову вийти, і т. Д .; а в кінцеву потрібно прийти, а якщо з неї потім і виходимо, то знову потрібно повернутися, і т. д.
Отже, щоб граф був унікурсальним, необхідно, щоб всі його вершини мали парний індекс або щоб число вершин з непарним індексом дорівнювало двом.
Тепер подивіться ще раз на граф завдання про кенігсберзькими мостах.
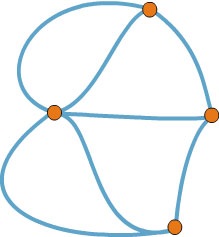
Мал. 5. Граф кенігсберзькими мостів
Порахуйте індекси його вершин і переконайтеся, що він ніяк не може бути унікурсальним. Ось тому-то у вас нічого не виходило, коли ви хотіли обійти всі мости.
Виникає питання: а якщо в зв'язковому графі немає вершин з непарним індексом або таких вершин рівно дві, то чи обов'язково граф унікурсален? Можна строго довести, що так! Таким чином, унікурсальность однозначно пов'язана з числом вершин з непарним індексом.
Вправа: побудуйте на схемі кенігсберзькими мостів ще один міст - там, де захочете - щоб отримані мости можна було б обійти, побувавши на кожному рівно по разу; реально виконайте такий шлях.
Ось вам ще кілька графів - порахуйте самі індекси вершин і, якщо це можливо, спробуйте обійти їх «не відриваючи олівця від паперу».
Модель 1. Унікурсальние графи
Тепер ще один цікавий факт: виявляється, будь-яку систему місцевостей, з'єднаних мостами, можна обійти, якщо необхідно побувати на кожному мосту рівно два рази! Спробуйте це довести самостійно.
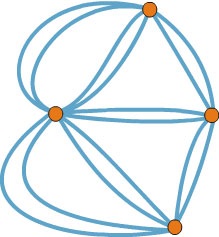
Мал. 6. Граф кенігсберзькими мостів з подвоєною кількістю мостів унікурсален