- 17.04.17 9:41 •
- FransuaMaryDelone •
- # 288176 •
- Гіктаймс •
- 33 •
- 1800
- такий же як Forbes, тільки краще.
збільшення
Почнемо, мабуть, з улюблених нами векторів. Властивість векторів - їх можна малювати в будь-якій точці простору, користуючись паралельним переносом - це властивість може здатися дивним. Як так. Навіщо це? І головне - з цим пов'язані різні смішні питання-вправи.
Наприклад: намалюйте в двовимірної декартовій системі координат вектор, який починається в точці (0,1) і має координати (1,0). У мене в групі не всі студенти могли це зробити (спасибі школі). Другий курс, між іншим. Вони ще фізиками себе називали гордо. Всілякі дурниці малювали ... зразок такого:
Тому все-таки зробимо це один раз. Намалюємо.
Наведемо цей «складний» алгоритм:
1. Відзначаємо точку, яка називається «координати вектора»;
2. малюємо вектор: проводимо стрілку з «нуля» в точку, яка називається «координати вектора»;
3. малюємо точку, яка називається «в ній починається вектор» - це буде «новий нуль» для нашого орієнтованого відрізка (вектора);
4. переносимо наш вектор на новий початок і садимо, щоб там ріс (паралельний перенос - називається).
б) І ще: ми не будемо говорити слово «довжина вектора» - це негарне слово. Воно негарне тому, що у «довжин» векторів бувають різні розмірності. Наприклад вектор сили має величину, що вимірюється в ньютонах, а величина вектора переміщення вимірюється в метрах. Щоб пам'ятати про різні величинах різних векторів, будемо себе завжди зупиняти. Ніколи не вимовляєте вголос мантру: «довжина вектора» - а то мова відвалиться (про себе думати можна про довжину, але недовго). Правильно говорити: «ВЕЛИЧИНА вектора» ... і будуть боятися злегка при цьому.
в) Отже ... Коли вимовляють слова «координати вектора», це означає, що його почали малювати з нуля. Це нам потім ще стане в нагоді, коли будемо векторне поле засівати. А зараз нам цей паралельний перенос знадобиться, щоб про збільшення поговорити.
Давайте подивимося на малюнок:
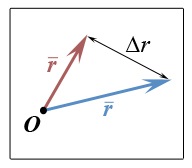
Тааак ... Якийсь синій вектор, якийсь червоний. Називаються однаково ... І між ними натягнута подвійна стрілка ... називається - вона не вектор - у неї немає початку, тільки два кінця. Взагалі ми тут про «збільшення» зібралися говорити. Тому пару слів про те, що у нас приростати буде. Математики все одно, що у нас приростає. Можна було б імена різні дати нашим векторах, потім відняти якийсь один з іншого і заспокоїтися. Але ми будемо називати обидва вектори однією літерою, а відрізняти їх будемо кольором. І говорити будемо про збільшення «цього вектора». Уявімо, що цей вектор якось змінюється, він для нас щось означає. Наприклад це вектор описує швидкість автомобіля або силу тертя ... Ну в загальному щось він означає таке, що залишається за кадром, але воно є - процес якийсь, рухається хтось або гроші витрачає, а може нагрівається - щось відбувається в загальному, а вектор описує це те, що відбувається. А інакше ці всякі збільшення взагалі не потрібні і безглузді. Загалом, хочеться звернути Вашу увагу на одну тонкість, а саме - на закон упорядкування.
Якщо ми намалюємо стрілку відрізку (ось так ось:), то можна сміливо назвати те, що вийде (а вийде у нас «дельта ер зі стрілкою»): - збільшенням вектора. Треба тільки зрозуміти «в яку сторону зростає» вектор. Треба якось пронумерувати що їх: синього і червоного. Хтось повинен взяти на себе сміливість і «поставити закон», тобто сказати, який вектор початковий, а який кінцевий. Ну давайте я пронумерує. Ось так вже краще:
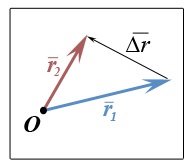
Так, мені здалося, що синій - це вектор початковий, а червоний - кінцевий. Ідея зрозуміла? - Нам потрібна якась причина, щоб упорядкувати вектори, щоб сказати, якою буде першим, а який другим. Зазвичай це якась природна причина, наприклад «час»: спочатку був один вектор, а потім інший. Або не "час» ... а «простір»: координата маленька - значить початок, а координата побільше - значить кінець. Але якесь міркування, якийсь закон нумерації векторів завжди потрібен. Так він і є завжди, тільки не завжди озвучується. Ось тут люди і помиляються з мінусом, в цьому місці - забувають стежити за законом, який впорядковує ... Ну а далі, як тільки такий закон є, то прирощення чогось (наприклад вектора, а може якогось скаляра або, прости Господи, тензора.) відразу автоматом обчислюється по одному єдиному монументальному правилом: «КІНЕЦЬ МІНУС ПОЧАТОК» - і це не переламати. Обов'язково з «кінця» віднімається «початок». У всіх випадках, завжди, вічно, у всіх алгоритмах. Це важливо пам'ятати, щоб не помилятися: спочатку закон упорядкування, потім «кінець мінус початок». Он подивіться на малюнок ще раз: з другого вектора відняли перший - перший показує початок, звідки росте «прирощення вектора», а встромляється «прирощення» в стрілочку другого вектора - все, кінець тут у вектора приросту. Тому що приріст - це «КІНЕЦЬ МІНУС ПОЧАТОК».
Зауважимо побіжно, що якби не паралельний перенос і не ось це ось «зневага» до початку і кінця вектора, то ми б такого красивого трикутнички НЕ намалювали. Довелося б все малювати з нуля. Їжачка йоржистого. Ось так:
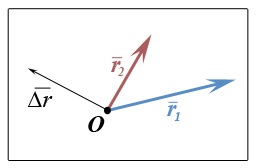
Це теж правильно, але менше наочно.
- А де базисні вектори. Чому тільки нуль намальований? - запитаєте ви.
Ну ... про системах координат ми трохи пізніше поговоримо. А тут їх не малюємо, щоб підкреслити, що це не має значення - не залежить від системи координат складання векторів - ми так захотіли, ми це придумали! Нам подобається, щоб не залежало додавання векторів від системи координат і немає на нас управи! Тут ми - боги! До речі, радіти рано, ми потім поплатимося за цю свою божественність, кожна наша «хотелка» тягне за собою відповідальність - це математика ж, а не фентезі яке-небудь.
- Але, дозвольте! - скажете Ви. - Яке додавання векторів. Де. Начебто ми з другого вектора вичитали перший вектор. Вичитали, а не складали!
Так, вичитали. А називаємо складанням, так. Ось так. Ми «складали». Просто один вектор ще і помножили на «мінус один» і підступно нічого не сказали про це. Ну давайте скажемо: Додавання і віднімання формально нічим не відрізняються, тому що вектор "" точно такий же повноцінний вектор, як і "" - у них навіть величина збігається, просто вони дивляться в різні боки. І все математичні формальні алгоритми до всіх векторах однаково добре ставляться, тому ці дві операції називають одним словом «складання» - це для стислості.
системи координат
Одна людина, маючи в кишені 100 денюшек, пішов на базар. Походив-подивився ... в одному кутку базару побачив кавуни по 2 денюшкі за штуку, а в іншому кутку кавуни були дорожче - 3 денюшкі за штуку. Ура! Можна нажитися на спекуляції! Купити дешевше, продати дорожче! На всі гроші! І так чотири рази!
Давайте намалюємо на графіку, як він чотири рази це все робив. Відзначимо точками на координатній площині цей процес з чотирьох кроків. Точки з'єднаємо стрілками ... Кавуни відкладемо по вертикалі, а денюшкі - по горизонталі. Та ще, щоб посмешнее було, похуліганити: зростання в зворотну сторону пустимо, не так як у всіх (інверсія системи координат у нас вийде). Спочатку людина перебувала в нульовому пункті: 100 денюшек і 0 кавунів, Це його точка «нуль»: (100,0). Потім він купив кавуни по 2 денюшкі за штуку на всі гроші! потрапив в точку «один»: (0,50), далі продав кавуни з вигодою: (150,0) і так чотири рази. Дивіться, яка краса виходить на графіку:
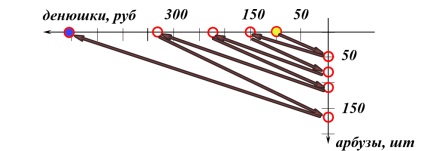
Як ви думаєте, он ті стрілочки, які кружечки з'єднують - це вектори?
кінець четвертого уроку. Далі буде.
Я погоджуся, що в разі афінність простору у нас дійсно суті розділені на вектора і точки, щоб не плутати їх один з одним. Це дійсно та область, де не можна просто так сказати, що це одне і те ж. Переконали.
Однак, погодьтеся, що це в цій конкретній абстракції. Коли ви оперуєте фізичними величинами, вам не важливо це поділ, так як безліч точок саме по собі є лінійним простором. Точно так же відмінності стираються в усіх застосуваннях над більшістю просторів. Тобто точка і вектор відрізняються термінологічно в рамках теорії Афінах просторів, але не відрізняються в застосуваннях.
Вважайте цей аргумент «останньої причіпкою». В цілому ваша аргументація прийнята.
А давайте більш конкретний приклад. Візьмемо в якості простору - стан твердого тіла в завданні механіки. У нас є 6 просторових координат (наприклад центр і 3 кута) і 6 швидкостей (нехай швидкість центру і 3 кутових швидкості). Рішення будь-якої задачі управління буде проводиться на цьому просторі, наприклад садимо ракету на баржу. А тепер два формулювання: візьмемо якусь точку цього простору, візьмемо деякий вектор в даному просторі. Я стверджую, що це абсолютно одне і те ж. І те й інше - 12 дійсних чисел, двенадцатіімерний вектор. Язик не повертається сказати двенадцатімерная точка. Однак в тій же задачі буде точка на фазовому портреті. Те ж простір, ті ж 12 вимірювань, але слово «точка».
Коли у нас є пряма геометрична інтерпретація, ще є сенс відрізняти вектор і точку. Але це тільки в малій кількості геометричних завдань, а в більшості навіть фізичних задач ця інтерпретація зникає. Ми починаємо векторно перемножать координати (точки в інтерпретації), поміщаємо об'єкти за координатами вектора і багато іншого. Наприклад ми можемо помножити векторно відносні координати об'єктів, щоб зрозуміти, хто правіше, а хто лівіше. Коли мова йде про безліч рухомих систем координат геть зникають відмінності векторів і точок.
Якщо беремо кути (повороту), то втрачаємо коммутативность складання. Тобто результат повороту на кут А, скажімо, навколо осі X, а потім на B навколо Y, це не те ж саме що спочатку поворот на B навколо Y, а потім на A навколо X.
Хм, ну і що? Як це заважає бути вектором некомутативної величиною? Вектор по одному з визначень - впорядкована множина. Є ще маса так чи інакше еквавалентних. Вектора чудово існують в будь-якому просторі, будь воно лінійним, Афіни або простором рожевих слонів. Комутативність - властивість лінійного простору, але зауважте, спочатку ми вводимо поняття вектора, операцій над ним, а потім вже коммутативность і простір.