Згладжує сплайн в mathcad

Згладжує сплайн в MathCAD

На відміну від інтерполяційного сплайна. що проходить через відомі точки i, fi> і вже реалізованого в MathCAD за допомогою вбудованих функцій interp і cspline. згладжує сплайн через вимірювання проходити не зобов'язаний. Зате він набагато гнучкіше і здатний, при відповідній настройці, компенсувати "аномальні" вимірювання або просто "загладити" дані не гірше МНК (точніше, краще - одиничний "викид" fi не «потягне" вгору або вниз весь згладжує сплайн, на відміну від полінома МНК зі статечним базисом).

Постановка завдання наступна: нехай на сітці x1

де h = x-xi - відстань до найближчого зліва вузла сітки, c3, i. c2, i. c1, i. i = 1, 2. N - 1 - коефіцієнти, що згладжує сплайна на i-му інтервалі по осі x. а yi - значення згладжує сплайна, обчислені в вузлах сітки xi. i = 1, 2. N.

У порівнянні з інтерполяційним сплайном, завдання обчислення коефіцієнтів згладжує сплайна набагато більш трудомістка і вимагає врахування додаткових параметрів, що впливають на ступінь згладжування:

речовинний масив df довжини N. dfi> 0. задає значення ваг в вузлах інтерполяції, чим більше вага вузла, тим сильніше буде загладжувати функція в його околицях. При відсутності додаткової апріорної інформації про відновлюваної залежності можна прийняти значення dfi однаковими, наприклад, рівними 1;
"Глобальний" параметр згладжування - дійсне значення sm (позначається також α), sm> 0. задає загальну міру згладжування даних - з його зростанням вона збільшується.

Вибір цих параметрів, взагалі кажучи, являє собою окрему задачу.

У пропонованому рішенні побудова сглажіваюшего сплайна реалізовано за допомогою двох функцій.

Функція SmoothSpline (x, f, df, sm) повертає об'єкт, що складається з матриці c коефіцієнтів згладжує сплайна розмірністю 3 * (N-1) і вектора y значень згладжує сплайна в вузлах сітки (розмірністю N). Код функції тут не наводжу через її громіздкість - півтори сторінки. Його можна побачити, завантаживши прикладений файл, а викликати функцію можна так:

виклик функції SmoothSpline

Зверніть увагу, що третій вимір "аномально", а інші представляють собою значення f (xi) = xi 2. Відповідно, завищений вага df3 (тут і далі елементи матриць і векторів нумеруються з одиниці, тому файл MathCAD починається визначенням системної змінної ORIGIN: = 1).

Також показаний непоганий (для невеликих значень N) спосіб вибору значення параметра згладжування sm.

Функція реагує на помилки у вихідних даних - такі, як кількість вузлів сітки, менше двох, і відсутність суворої впорядкованості по зростанню значень xi.

Функція додатково використовує тільки службовий речовинний масив r розмірністю 7 * (N + 2). тобто, досить економічна по пам'яті.

Тест і результат по ньому звірений з матеріалами науково-дослідного обчислювального центру МДУ, все збіглося :)

Друга функція - GetSmoothSpline (x, dx, y, c) займається побудовою згладжує сплайна за відомою матриці коефіцієнтів c і значенням сплайна yi в вузлах сітки xi. аргумент x всередині функції змінюється від x1 до xlength (x) з кроком dx. Функція поверне матрицю з двох вектор-стовпців - в першому міститимуться значення аргументу, у другому - обчислені значення сплайна. Скористатися функцією і потім наочно вивести результати згладжування можна, наприклад, так:

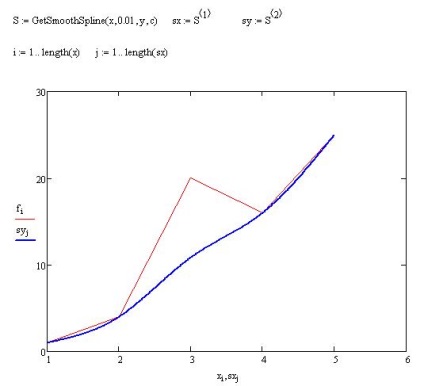
виклик функції GetSmoothSpline

Як другий приклад покажемо, як згладжує сплайн вміє справлятися з "аномальними" вимірами, що виникають в результаті діяльності ворогів народу будь-яких збоїв і не вписуються в "загальну картину".

Дані на цей раз сгенерируем програмно, просто "знявши" їх з шматочка синусоїди, потім пару вимірювань зробимо сильно відрізняються від інших:

дані з "аномальними" вимірами

Ось як впорався згладжує сплайн з цими двома геями "викидами":

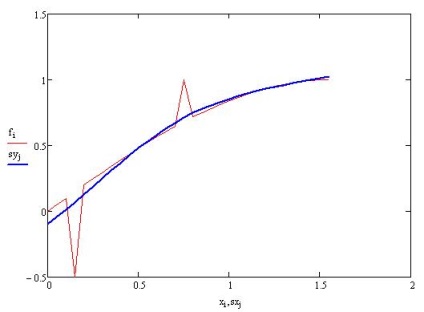
обробка даних з аномальними вимірами, згладжує сплайн

Видно, що відхилень він майже не помітив.

Ну а хочете ще краще - обґрунтовано вибирайте ваги вузлів і параметр згладжування.

Зрозуміло, що згладжує сплайн не всесильний - наприклад, якщо "перемельчіть" сітку і переборщити з кількістю "аномалій", він може піти "рознос", тоді для обробки таких даних доведеться залучати апарат, здатний врахувати якісні апріорні обмеження ( "а ось на цьому інтервалі функція повинна зростати! "). Такий апарат відомий як дескриптивні сплайни, але статей про них я не писав уже давно, може, коли-небудь :)