Ми можемо записати їх в матричної формі:
- матриця податливості (квадратна матриця розмірності (6х6);
() - елементи матриці податливості.
матриця піддатливості # 916; однозначно і повністю описує жорсткісні характеристики розглянутого пружного елемента (в даному випадку стержня).
Елемент матриці податливості () - це величина, що чисельно дорівнює переміщенню в -ом напрямку при дії одиничної сили в -ом напрямку:
- діагональні елементи характеризують податливість стрижня в напрямку діючої сили;
при - ці елементи характеризують лінійну податливість стрижня (розмірність елементів [м / Н]);
при - ці елементи характеризують кутову податливість стрижня (розмірність елементів [1 / мН]);
при. і при . - ці елементи характеризують перехресні зв'язки між кутовими і лінійними переміщеннями полюса (розмірність елементів [1 / Н]).
Інтеграл Мора, що описує переміщення () довільної точки пружного стержня при дії зовнішнього навантаження,
де - відповідні внутрішні зусилля, що виникають від дії зовнішнього навантаження;
() - відповідні внутрішні зусилля, що виникають від дії в полюсі одиничної навантаження ().
На підставі інтеграла Мора і вирази (1.5) запишемо формулу для визначення елементів () матриці податливості:
Згідно виразу (1.6) є очевидним, що ().
Повернемося до вираження (1.4):
Помножимо ліву і праву частини виразу (2.1) на
Тоді, позначивши матрицю жорсткості, отримаємо рівняння рівноваги в матричному вигляді
Тут - мінор матриці (визначник подматріци, яка виходить з даної матриці викреслюванням -ої рядки і-го стовпця).
Приклад розрахунку матриці податливості прямолінійного стержня:
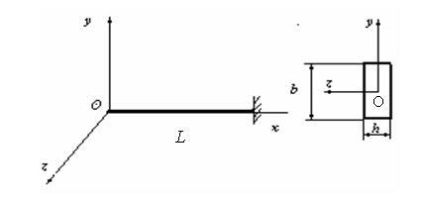
В даному випадку
1. Розглянемо випадок, коли i = 1.
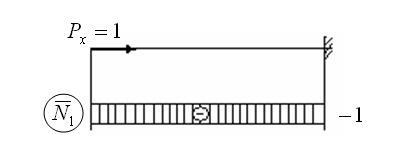
2. Розглянемо випадок, коли і = 2
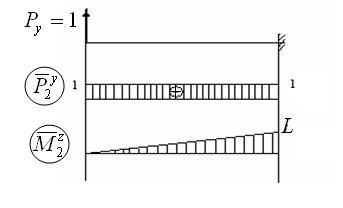
3.Расмотрім випадок, коли і = 3:
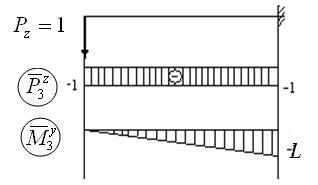
4.Рассмотрім випадок, коли і = 4:
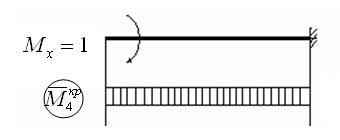
5.Рассмотрім випадок, коли і = 5:
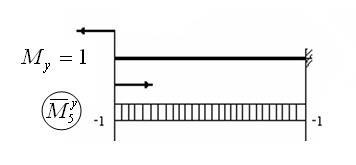
6. Розглянемо випадок, коли і = 6:
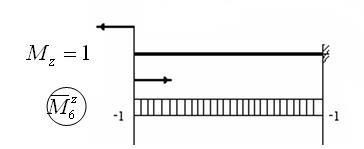
Тоді згідно з формулою (1.6) отримуємо:
Розглянемо матрицю податливості прямолінійного пружного елемента, що має змінну по довжині перетин. Пружний елемент складається з двох ділянок: М і Е.
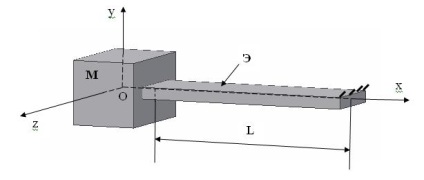
Розглядаємо матрицю податливості в системі координат Oxyz.
- площа поперечного перерізу інерційної маси;
- площа поперечного перерізу пружного елемента;
Розглянемо деякі властивості парних і непарних функцій.
1) Якщо А (х) -четная функція, т. Е. А (х) = А (х) (наприклад А (х) = х 2), то.
2) Якщо А (х) - непарна функція, тобто А (х) = - А (х) (наприклад А (х) = х),
Якщо розташувати полюс посередині (;) стержня, тоді, використовуючи властивість непарної функції, можемо записати
Значить, якщо прямолінійний стержень має постійний перетин по довжині стрижня, а полюс розташований посередині і при цьому жорстко пов'язаний з незакріпленим кінцем стержня, то матриця податливості має діагональну форму.
У разі діагональної матриці податливості маємо переміщення полюса тільки в напрямку дії сили.
Для пружних елементів постійного перерізу в разі розташування полюса в точці, яка відповідає центром недеформованого стрижня, отримуємо:
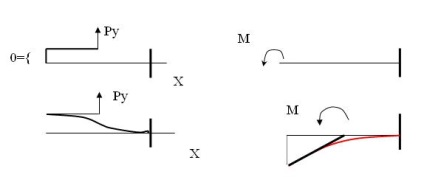
Система координат, в якій матриця піддатливості пружного елемента має діагональну форму, носить назву системи нормальних координат.
В системі нормальних координат при дії в полюсі узагальненої сили, переміщення відбувається тільки в напрямку дії сили
Визначимо елементи матриці податливості УЕ постійного перетину в системі координат, щодо осей і центра якої УЕ володіє симетрією.
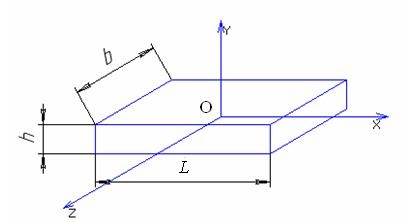
Для даного УЕ матриця податливості матиме діагональну форму.