Цей пост навіяний ось цим завданням.
Виявляється, зірок, зірчастим багатокутників і многогранників присвячено безліч цікавих статей та цілих сайтів.
Те, що ви бачите, взято ось з цього чудесного сайту: zvzd3d.ru/. І це лише мала-мала частина. Чого там тільки немає!
Але спочатку розберемося з плоскими зірками.
У Вікіпедії про зірок написано ось що:
Зірка - певний вид плоских неопуклих багатокутників, що не має, однак, однозначного математичного визначення. Зазвичай під зірками на увазі фігури, що нагадують за формою зображення зірки.
І відразу після цього дається цілих два визначення.
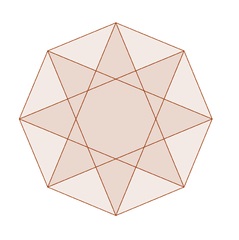
Правильна 8-верхова зірка, вписана в правильний 8-кутник
Визначення 2. Зірчастий багатокутник
Кожна вершина правильного n-багатокутника з'єднаються з m-ної від неї на окружності за годинниковою стрілкою. Зірка, отримана таким чином, позначається як. При цьому точки перетину сторін між собою не розглядаються як вершини. Така зірка має n вершин і n сторін, також як і правильний n-кутник. Її також називають зірчасті многоугольником, і вона є зірчастої формою відповідного їй n-кутника.


П'ятикутна зірка, вписана в правильний п'ятикутник і Пентаграма Пенроуза
Зірки можуть бути зв'язковими (нераспадающіхся єдиними багатокутниками), яка є сполуками інших правильних або зірчастих многокутників, а можуть бути незв'язними. розпадаючись на кілька однакових правильних багатокутників або зв'язкових зірок.
Двовимірне дискретне безліч зірок
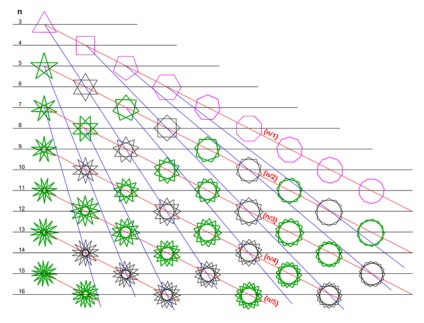
Пурпурні - опуклі багатокутники.
Зелені - зв'язкові зірки (де n і m взаємно прості числа).
Чорні - НЕ зв'язкові зірки (де n і m не взаємних прості числа).
Сині прямі з'єднують багатокутник (опуклий або зв'язну зірку) зі всіма не зв'язковими зірками, які є сполуками (після повороту) різної кількості однакових багатокутників, таких же як цей.




Зірчастий багатогранник (зірчасті тіло) - це неопуклих багатогранник, грані якого перетинаються між собою. Як і у незвёздчатих багатогранників, грані попарно з'єднуються в ребрах, при цьому внутрішні лінії перетину не зважають ребрами.
Зірчастої формою многогранника називається багатогранник, отриманий шляхом продовження граней даного багатогранника через ребра до їх наступного перетину з іншими гранями за новими ребрах.
Правильні зірчасті багатогранники - це зірчасті багатогранники, гранями яких є однакові правильні або зірчасті багатокутники. Коші встановив, що існує всього 4 правильних зірчастих тіла, які не є сполуками платонових і зірчастих тіл, звані тілами Кепплера - Пуансо: все 3 зірчастих форми Додекаедр і одна з зірчастих форм ікосаедра. Решта правильні зірчасті багатогранники є або з'єднаннями платонових тел, або сполуками тел Кепплера - Пуансо.
Багато форми зірчастих багатогранників підказує сама природа. Наприклад, сніжинки - це плоскі проекції зірчастих багатогранників. Деякі молекули мають правильні структури об'ємних фігур.
Напівправильні зірчасті багатогранники - це зірчасті багатогранники, гранями яких є правильні або зірчасті багатокутники, але не обов'язково однакові. При цьому будова всіх вершин має бути однаковим (умова однорідності). Коксетер і інші до 1954 року перерахували 53 таких тіла і висунули гіпотезу про повноту свого списку. Тільки значно пізніше вдалося довести, що отриманий ними список багатогранників дійсно повний.
Однорідні багатогранники - правильні і напівправильні опуклі багатогранники (Платонова і архімедовим тіла), правильні і напівправильні зірчасті багатогранники разом називаються однорідними многогранниками. У цих тіл всі грані є правильними багатокутниками (опуклими або зірчастими), а всі вершини однакові (тобто існують ортогональні перетворення багатогранника в себе, що переводять будь-яку вершину в будь-яку іншу). Існує рівно 75 однорідних багатогранників.
Даю посилання на статтю у Вікіпедії, тому що привела тільки малу частину картинок і малу частину відомостей!
зірчасті багатогранники
Ще кілька посилань.
1. Сайт Зірчасті багатокутники dorigami.narod.ru/dorigami_rco.html
2. Вікіпедія Пентаграмма
3. Вікіпедія Гексаграмма
4. Вікіпедія октаграма
5. Сайт многограннікі.ру