1. Знаходження структури дотичного портфеля.
2. Розподіл капіталу між дотичним портфелем і безризиковими активом відповідно до індивідуальної схильністю до ризику.
Можливість роздільного вирішення завдань оптимізації ризикової частини портфеля і портфеля в цілому відомо як теорема про поділ.
До тих же висновків призводить і формальне математичне рішення задачі Тобіна, наведене, наприклад в [3, стр.109-113] (розглянуті випадки залучення позик і без них). Крім класичних формальних методів вирішення задачі Тобіна існують "спеціалізовані", засновані на використанні теореми про поділ, тобто на початковому знаходженні дотичного портфеля. Наприклад, можна використовувати вже згадуваний метод критичних ліній або описаний в [4, стр.253-256] метод EGP, названий за іменами творців Елтона, Грубера і Падберг (метод використовує властивість дотичного портфеля мати максимальний кут нахилу прямої, що з'єднує відповідну йому точку з точкою безризиковою прибутковості).
Макроекономічне значення результатів Тобіна полягає в моделюванні попиту на гроші при зміні прибутковості ризикових активів.
Хоча припущення Тобіна про можливість чисто безризикових вкладень на практиці строго не здійснимо, рішення задачі Тобіна з використанням слаборіскових активів виявляється близьким до розрахункового і тому має практичне значення [3, стор.112].
2.4. Модель CAРM і її узагальнення
На самому початку 60-х років учнем Марковіца У. Шарпом була запропонована так звана однофакторний модель ринку капіталів, в якій вперше з'явилися знамениті згодом "альфа" і "бета" - характеристики акцій. На основі однофакторний моделі Шарп згодом запропонував спрощений метод вибору оптимального портфеля, який зводив задачу квадратичної оптимізації до лінійної. У найпростіших випадках, для невеликих розмірностей, ця задача могла бути вирішена практично "вручну". Таке спрощення зробило методи портфельної оптимізації застосовними на практиці. До 70-их рр. розвиток програмування, а також удосконалення статистичної техніки оцінювання показників "альфа" і "бета" окремих цінних паперів та індексу прибутковості ринку в цілому призвело до появи перших пакетів програм для вирішення задач управління портфелем цінних паперів.
Спочатку Шарпом переслідувалася мета спростити отримання вихідних даних (перш за все, ковариаций між прибутковістю цінних паперів), необхідних для вирішення задачі оптимізації портфеля по Марковіцу. Для цього була використана однофакторний модель залежності дохідності довгостроковій ризикової цінного паперу від фактора - середньозваженої по капіталізації фондових активів прибутковості ринку:
де - загальне число всіх обертаються на ринку цінних паперів,
- відповідно частка в загальній капіталізації ринку і прибутковість -ої цінного паперу.
Однофакторна модель прибутковості -ої цінного паперу будується як лінійна регресійна залежність, одержувана за методом найменших квадратів:
де - коефіцієнт зміщення регресійній моделі, що відображає активну прибутковість - додаткову прибутковість даного цінного паперу щодо - і ступінь інтересу інвесторів до неї,
- коефіцієнт чутливості зміни прибутковості цінних паперів щодо зміни прибутковості середньоринкового портфеля,
- похибка регресійній моделі, яка відображає вплив усіх інших факторів.
Регресійна залежність будується в припущенні про залежність доходностей всіх цінних паперів тільки від одного фактора - і, отже, взаємної некоррелированности помилок, а з алгоритму методу найменших квадратів слід, що
де - СКО відповідно доходностей -ої цінного паперу і середньоринкового портфеля,
- коефіцієнт кореляції між прибутковістю -ої цінного паперу і прибутковістю середньоринкового портфеля.
Якщо відомі коефіцієнти для всіх ризикових фондових активів (а до висновку про необхідність їх оцінки з огляду на наочності практика фондового ринку прийшла досить швидко), то ковариации доходностей цінних паперів і їх дисперсії можуть бути обчислені застосуванням правил теорії ймовірностей до (2.12):
Ці правила легко узагальнюються на випадок портфеля, що складається з ризикових цінних паперів, представлених в ньому частками:
Ризик портфеля визначається:
Перший доданок в (2.20) характеризує ринковий (систематичний, недіверсіфіціруемий) ризик. а друге - власний ризик портфеля, який може бути зменшений за рахунок диверсифікації як показано на рис.2.7.
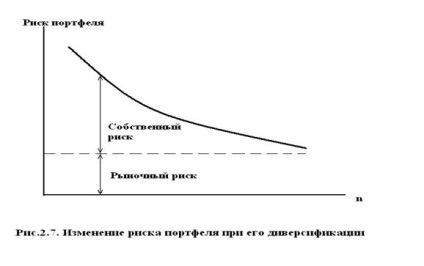
Однак по-справжньому значуще наукове і практичне значення регрессионная апроксимація у вигляді (2.12) і (2.13) отримала в зв'язку з використанням результатів Тобіна для моделювання ціноутворення довгострокових активів на фондовому ринку.
З 1964 р з'являються роботи Шарпа, Дж.Лінтнера, Моссіна, що відкрили наступний етап в інвестиційній теорії, пов'язаний з так званої моделлю оцінки капітальних активів, або САРМ (Capital Asset Pricing Model). Результати, отримані в цих роботах, засновані на вихідних припущеннях Марковіца (див. П.2.2), доповнених наступними:
1. Для всіх інвесторів період вкладення однаковий.
2. Інформація вільно і негайно доступна для всіх інвесторів.
3. Інвестори мають однорідні очікування, тобто однаково оцінюють майбутні прибутковості, ризик і коваріації доходностей цінних паперів.
4. Безризикова процентна ставка однакова для всіх інвесторів
У сукупності всі вихідні припущення описують так званий досконалий ринок цінних паперів, на якому відсутні перешкоджають інвестиціям чинники. Є ще одне положення CAРM, яке зазвичай вважають наслідком теореми про поділ: в стані рівноваги кожен вид цінних паперів має ненульову частку в дотичному портфелі, а структура дотичного портфеля повторює структуру ринкового портфеля відповідно до часток капіталізації цінних паперів. Обгрунтуванням служить наступне міркування: якщо дотичний портфель одного інвестора не включає якийсь папір, це означає, що її намагаються продати все (так як інвестори купують однакові за структурою ризикові складові своїх портфелів), тоді ринковий курс цього паперу під тиском надлишкової пропозиції буде падати , а очікувана прибутковість відповідно зростати - до тих пір, поки ціна не стане рівноважної, а частка в дотичному портфелі - відмінною від нуля. Протилежні події будуть відбуватися при спробі інвесторів (всіх одночасно) збільшити частку якогось паперу в ризиковій частині вкладень.
На основі останнього твердження і використовуючи (2.11) можна записати вираз для очікуваної прибутковості фінансових коштів будь-якого інвестора в стані рівноваги ринку:
де, як і раніше, - прибутковість і ризик середньоринкового (дотичного) портфеля,
- прибутковість безризикових активів
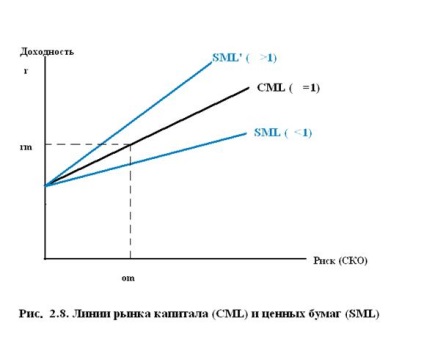
(2.22) описує ефективний фронт Тобіна (рис.2.8) і отримало назву рівняння ринку капіталу (Capital Market Line - CML). При цьому величина
дорівнює тангенсу кута нахилу CML до осі ординат і відображає збільшення прибутковості при збільшенні ризику на одиницю, тобто граничну прибутковість ризику вкладень ринку при наявності ризикових і безризикових активів. Оскільки CML стосується ефективного фронту Марковіца в точці, можна висловити тангенс нахилу дотичній через вираження. описує фронт Марковіца. Цей вислів отримано в [Гр] і має вигляд:
,
де ставляться до будь-якої з цінних паперів портфеля,
- коефіцієнт кореляції прибутковості цього цінного паперу і портфеля в цілому.
Прирівнюючи праві частини двох останніх виразів, можна отримати вираз для очікуваної прибутковості будь-якого цінного паперу в оптимальному портфелі:
яке називається рівнянням лінії ринку цінних паперів (Security Market Line - SML) і з урахуванням (2.13) може бути переписано з використанням коефіцієнта:
Різниця називають премією за недиверсифікований ризик тримання ринкового портфеля, відповідно різниця - премія за ризик тримання окремо ¿ризикового активу, а бета показує внесок кожного цінного паперу в ризик ринкового портфеля.
Порівняння виразів для CML та SML показує, що ці лінії на площині збігаються тільки при. При лінія SML проходить вище, а при - нижче лінії CML (рис.2.8). У будь-якому випадку активи з великим ризиком повинні забезпечувати пропорційно більшу прибутковість. Таким чином, якщо портфель ефективний, зв'язок між очікуваною прибутковістю кожної акції і її граничним внеском в портфельний ризик повинна бути прямолінійною. Вірно і зворотне: якщо прямолінійною зв'язку немає, портфель не є ефективним.
Використовуючи рівняння SML, можна визначити факт недооцінки або переоцінки цінних паперів (наприклад, акції) не тільки по її прибутковості, але і порівнянням її дійсного курсу і курсу відповідно до рівноважної ціною ризику, який позначимо через. Нехай очікувана в кінці деякого майбутнього періоду ціна акції (з огляду на дівідентний дохід) дорівнює. Прирівнюючи вирази прибутковості по визначенню і за рівнянням SML, отримаємо:
,
звідки слід відома формула дисконтування за безризиковою прибутковості, збільшеної на ризикову надбавку:
.
Узагальнюючи викладене, можна вважати САРМ макроекономічним узагальненням теорії Марковіца, що дозволяє встановити співвідношення між прибутковістю і ризиком активу для рівноважного ринку. При цьому важливим виявляється той факт, що при виборі оптимального портфеля інвестор повинен враховувати не "весь" ризик, пов'язаний з активом (ризик за Марковіцу), а тільки Недіверсіфіціруемий його частина. Ця частина ризику активу тісно пов'язана із загальним ризиком ринку в цілому і кількісно представляється коефіцієнтом "бета", введеним Шарпом в його однофакторний моделі. Інша частина (несистематичний, або діверсіфіціруемий ризик) усувається вибором відповідного оптимального портфеля. Характер зв'язку між прибутковістю і ризиком має вид лінійної залежності. Якщо інвестори не мають будь-якої додаткової інформацією, їм слід тримати такий же портфель акцій, як і у інших - тобто ринковий портфель цінних паперів.
У 1977 році ця теорія зазнала критики в роботах Річарда Ролла. Ролл висловив думку, що САРМ слід відкинути, оскільки вона в принципі не допускає емпіричної перевірки. Існує досить багато заперечень проти обґрунтованості положень CAPM, найбільш спірними з них вважаються [4] припущення:
Інформація про роботу «Теорія ефективних фондових інвестицій та її застосування (розділ дипломної роботи)»
Розділ: Фінанси
Кількість знаків з пробілами: 34191
Кількість таблиць: 0
Кількість зображень: 9