Загальна теорія для обчислення площі квадрата.
Квадрат - це правильна плоска фігура, що складається з чотирьох точок, три з яких не лежать на одній прямій, і чотирьох відрізків, що з'єднують попарно ці чотири точки, всі сторони і кути якої рівні.
Точки називаються вершинами квадрата і позначаються великими латинськими літерами.
Відрізки називаються сторонами квадрата і позначаються парою заголовних латинських букв відповідно вершин, які відрізки з'єднують.
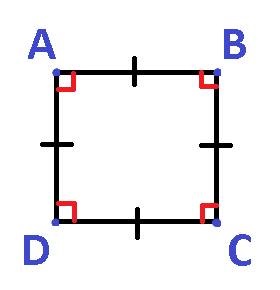
На малюнку №1 представлений квадрат ABCD з вершинами A, B, C, D і сторонами AB, BC, CD, DA.
Кут, утворений променями AB і AD, називається кутом при вершині A. Позначається він як ∠A або ∠BAD, або ∠DAB.
Кут, утворений променями BA і BC, називається кутом при вершині B. Позначається він як ∠B або ∠ABC, або ∠CBA.
Кут, утворений променями CB і CD, називається кутом при вершині C. Позначається він як ∠C або ∠DCB, або ∠BCD.
Кут, утворений променями AD і CD, називається кутом при вершині D. Позначається він як ∠D або ∠ADC, або ∠CDA.
Як видно з визначення, сторони квадрата рівні (AB = BC = CD = DA). Кути квадрата теж між собою рівні (∠A = ∠B = ∠C = ∠D) і складають 90 0.
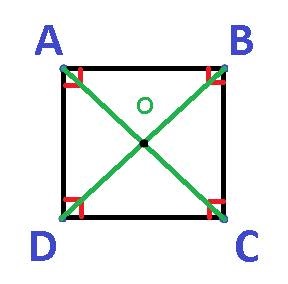
На малюнку №2 відрізки AC і BD називаються діагоналями квадрата.
Діагоналі квадрата перетинаються і точкою перетину діляться навпіл. Тобто, AO = CO = BO = DO.
Діагоналі квадрата ділять кути, з яких вони виходять, навпіл.
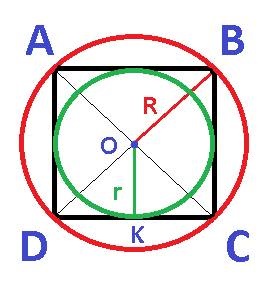
Малюнок №3: Квадрат ABCD з вписаною і описаної окружністю.
Центр вписаного і описаного кола співпадають і лежать в точці перетину діагоналей квадрата.
На малюнку №3 відрізок ОК - радіус r вписаного в квадрат кола, а відрізок ОВ - радіус R описаного навколо квадрата окружності.
Якщо позначити сторону квадрата буквою a. діагональ буквою d. то справедливі такі співвідношення:
1. Радіус r вписаною в квадрат кола дорівнює половині сторони a квадрата.
2. Радіус R описаного навколо квадрата кола дорівнює половині діагоналі квадрата. Так як діагональ квадрата d пов'язана з стороною співвідношенням, то нескладно отримати залежність радіуса описаного навколо квадрата окружності і його боку:
Площею S плоскої фігури, до яких відноситься і квадрат, називається обмежене замкнутий простір на площині. Площа плоскої фігури показує величину цієї фігури.
Площа володіє декількома властивостями:
1. Вона не може бути негативною.
2. Якщо дана деяка замкнута область на площині, яка складена з декількох фігур, які не перетинаються один з одним (тобто, фігури не мають спільних внутрішніх точок, але цілком можуть торкатися один одного), то площа такої області дорівнює сумі площ складових її фігур .
3. Якщо дві фігури рівні, то і площі їх рівні.
4. Площа квадрата, який побудований на одиничному відрізку, дорівнює одиниці.
За едініцуізмереніяплощаді приймають площу квадрата, сторона якого дорівнює едініцеізмеренія відрізків.
При вирішенні завдань часто використовуються наступні формули обчислення площі квадрата:
1. Площа квадрата дорівнює квадрату його сторони:
2. Площа квадрата дорівнює половині квадрата його діагоналі:
3. Площа квадрата дорівнює чотирьом квадратах радіуса вписаного кола:
4. Площа квадрата дорівнює двом квадратах радіусу описаного кола:
Приклад 1: Обчислити площу квадрата зі стороною a = 3.
Для знаходження площі квадрата скористаємося формулою обчислення площі квадрата:
Таким чином, маємо наступне:
Приклад 2: Знайти сторону квадрата з площею S = 144 см 2.
Для знаходження сторони квадрата скористаємося формулою обчислення площі квадрата:
Висловимо з цієї формули сторону квадрата:
Таким чином, маємо наступне:
Приклад 3: Обчислити площу квадрата з діагоналлю d = 6.
Для знаходження площі квадрата скористаємося формулою обчислення площі квадрата:
Таким чином, маємо наступне:
Приклад 4: Знайти діагональ квадрата з площею S = 32 см 2.
Для знаходження діагоналі квадрата скористаємося формулою обчислення площі квадрата:
Висловимо з цієї формули діагональ квадрата:
Таким чином, маємо наступне:
Приклад 5: Обчислити площу квадрата, якщо радіус вписаного в нього кола r = 5.
Для знаходження площі квадрата скористаємося формулою обчислення площі квадрата:
Таким чином, маємо наступне:
Приклад 6: Знайти радіус вписаного в квадрат кола, якщо його площа S = 225.
Для знаходження радіуса вписаного в квадрат кола скористаємося формулою обчислення площі квадрата:
Висловимо з цієї формули радіус вписаного в квадрат кола:
Таким чином, маємо наступне:
Приклад 7: Обчислити площу квадрата, якщо радіус описаного навколо нього кола R = 7.
Для знаходження площі квадрата скористаємося формулою обчислення площі квадрата:
Таким чином, маємо наступне:
Приклад 8: Знайти радіус описаного навколо квадрата кола, якщо його площа S = 200.
Для знаходження радіусу описаного навколо квадрата кола скористаємося формулою обчислення площі квадрата:
Висловимо з цієї формули радіус описаного навколо квадрата кола:
Таким чином, маємо наступне: