Рішення оптимізаційної задачі
Можна сказати, що сполучений функтор - це спосіб вказівки найбільш ефективного вирішення певної проблеми за допомогою стандартного методу. Наприклад, елементарна проблема з теорії кілець - як перетворити псевдокольцо (тобто кільце, яке може не мати мультипликативной одиниці) в кільце. Найбільш ефективний спосіб це зробити - додати в кільце одиницю, всі елементи, необхідні для виконання аксіом кільця (наприклад, елементи типу r +1. Де r - елемент кільця) і не припускати ніяких співвідношень в новому кільці, які не потрібні для виконання аксіом. Ця конструкція стандартна в тому сенсі, що вона працює для будь-якого псевдокольца.
Сказати, що цей метод визначає «найбільш ефективне» і «стандартне» рішення проблеми - те ж саме, що сказати, що він задає зв'язані функтори.
Існують кілька еквівалентних визначень сполучених функторів. Їх еквівалентність елементарна, але не тривіальна.
Визначення за допомогою універсальної стрілки [⇨] легко сформулювати, воно також найближче до нашої інтуїції з приводу «оптимізаційної задачі».
Визначення за допомогою одиниці і коедініци [⇨] зручно для функторів, часто зустрічаються в алгебрі, тому що надає формули, які можна перевірити безпосередньо.
Визначення за допомогою множин Hom [⇨] робить очевидною симетричність визначення і прояснює причини для іменування функторів «сполученими».
Універсальна стрілка
Як і має на увазі термінологія, вірно, що F - лівий зв'язаний для G тоді і тільки тоді, коли G - правий зв'язаний для F. Однак це не очевидно з визначення через універсальну стрілку, але очевидно завдяки визначенню через одиницю і коедініцу.
Одиниця і коедініца
званих відповідно коедініцей і одиницею сполучення, таких що композиції
є тотожними перетвореннями 1F і 1G функторів F і G відповідно.
У такій ситуації F є лівим сполученим для G і G є правим сопрядённим для F. Іноді це відношення позначають (ε. Η). F ⊣ G або просто F ⊣ G.
У формі рівнянь наведені вище умови на (ε, η) називаються рівняннями коедініци і одиниці:
1 F = ε F ∘ F η 1 G = G ε ∘ η G 1 _ = \ varepsilon F \ circ F \ eta \\ 1_ = G \ varepsilon \ circ \ eta G \ end >>
Визначення через функторів Hom
Це визначає сімейство біекція:
для всіх об'єктів X в C і Y в D.
Тут F називається лівим сполученим для G і G - правим зв'язаних для F.
Щоб зрозуміти, що мається на увазі під природністю Φ. потрібно пояснити, яким чином homC (F -, -) і homD (-, G -) є функторами. Насправді, вони обидва є біфункторамі з D op × C в Set. В явному вигляді природність Φ означає, що для всіх морфізма f. X → X 'в C і морфізма g. Y '→ Y в D наступна діаграма комутує:
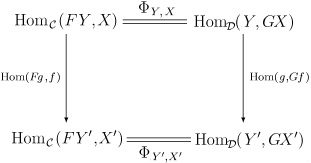
вільні групи
Конструкція вільної групи є зручним прикладом для прояснення суті визначень. Нехай F. Grp ← Set - функтор, який безлічі Y зіставляє вільну групу, породжену елементами Y. і G. Grp → Set - забуває функтор. сопосталяющій групі X її безліч-носій. Тоді F - лівий зв'язаний для G:
Термінальні стрілки: для кожної групи X. група FGX - вільна група, породжена елементами X як безліччю. Нехай ε X. FGX → X: FGX \ to X> - гомоморфізм груп, який переводить утворюють FGX до відповідних елементів X. Тоді (G X. ε X))> - термінальний морфізм з F в X. тому що будь-який гомоморфізм з вільної групи FZ в X проноситься через ε X. FGX → X: FGX \ to X> за допомогою єдиної функції з безлічі Z в безліч X. Це означає що (F, G) - пара сполучених функторів.
Безлічі Hom: відображення з вільної групи FY в групу X однозначно відповідають відображенням безлічі Y в безліч GX. кожен гомоморфізм однозначно визначається своїми значеннями на утворюють вільної групи. Прямим обчисленням можна перевірити, що це відповідність - природне перетворення, а значить пара (F, G) сполучена.
Подальші приклади з алгебри
Приклади з топології
існування
де індекси i пробігають безліч I. таке що будь-який морфізм:
може бути записаний як:
для деякого i в I і деякого морфізма:
Аналогічне твердження характеризує функтори, що мають правий зв'язаний.
Единственность
В іншу сторону, якщо F пов'язаний зліва до G. і G природно ізоморфний G '. то F також пов'язаний зліва до G '.
композиція
Композиції сполучень можна брати природним чином. Якщо
пов'язаний зліва до функтором