На практиці дуже часто необхідно вміти вирішувати зворотну задачу: якими мають бути абсолютні похибки аргументів функції, щоб абсолютна похибка функції не перевищувала заданої величини.
Нехай величина граничної абсолютної похибки задана.
Припускаючи, що всі складові рівні між собою, будемо мати:
У разі, коли гранична абсолютна похибка всіх аргументів одна і та ж, то:
7.1. Радіус основи циліндра; висота циліндра. З якими абсолютними похибками потрібно визначити R і Н, щоб обсяг циліндра V можна було вирахувати з точністю до 0,1 м?
Обсяг обчислюється за формулою і. Підставляючи всі вихідні дані, наближено одержимо:
Звідси, т. К. П = 3, то, скориставшись формулою для обчислення похибкою-ності функції, що залежить від трьох змінних:
Таблиця Похибки значень елементарних функцій.


8. Завдання до лабораторної роботи № 1:
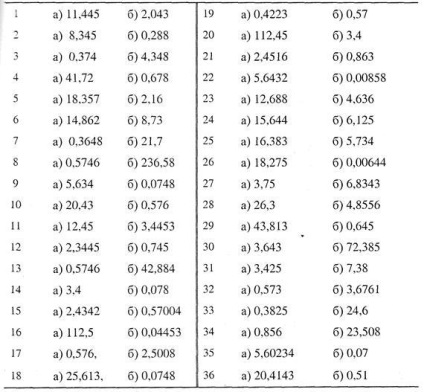
8.1. Завдання (самостійно) .Знайти граничні абсолютні і відносні похибки чисел, якщо вони мають тільки вірні цифри (таблиця варіантів завдання).
а) в строгому сенсі; б) в широкому сенсі.
Табліца.Варіанти завдань для виконання самостійної роботи
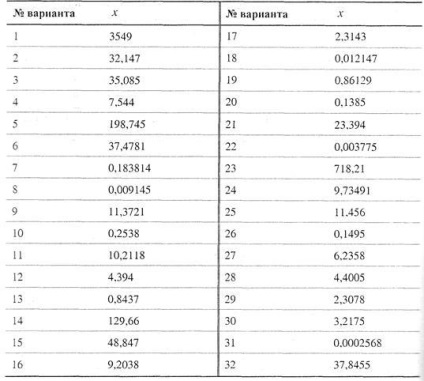
8.2. Завдання для самостійної роботи. Число х (табл.), Всі цифри якого вірні в строгому сенсі, округлити до трьох значущих цифр. Для отриманого результату обчислити межі абсолютної і відносної похибок. У записі числа. вказати кількість вірних цифр по абсолютній і відносній погрішності.
Табліца.Варіанти завдань для виконання самостійної роботи
8.3. Обчислити значення величини z (табл) при заданих значеннях чисел а. b і з використовуючи систематичний облік абсолютних похибок після кожної операції, а також за допомогою методу кордонів. Знайти абсолютну і відносну похибки z і визначити по ним кількість вірних цифр в z, якщо цифри а. b і з вірними в строгому сенсі.
Таблиця. Варіанти завдань для виконання самостійної роботи




8.4. Вирішити такі завдання, використовуючи метод кордонів.
8.4.1. Довжина повітряної траси між двома пунктами дорівнює S км. Літак долає цю відстань за час t ч. Визначити кордону середньої швидкості літака, якщо:; .
8.4.2. Електроплитка розрахована на напругу В. Знайти опір спіралі електроплитки, якщо відомо, що через неї повинен пройти струм 5 ± 0,1 А.
8.4.3. Мідний брусок має обсяг V м (). Знайти його масу, якщо щільність міді кг / м становить.
8.5. Вирішити такі завдання, використовуючи загальну формулу похибки.
8.5.1. Питомий електричний опір металу круглого дроту завдовжки l м з поперечним перерізом d мм і опором R Ом визначається за формулою:. Знайти. якщо: l = 12,50 ± 0,01 м, d = 2,00 ± 0,01 мм, R = 0,068 ± 0,0005 Ом, = 3,141 ± 0,001. Визначити відносну похибку.
8.5.2. Вертикальний циліндричний резервуар наповнений рідиною. Визначити час, необхідний для спорожнення резервуара через круглий отвір в дні. Діаметр резервуара D = 1 ± 0,01, висота рівня рідини H = 2 ± 0,02 м, діаметр отвору дна d = 0,03 ± 0,001, коефіцієнт витрати = 0,6 ± 0,02. Розрахунок (в секундах) ведеться за формулою:
8.6. Вирішити такі завдання, використовуючи зворотну задачу теорії похибок:
8.6.1. З якою точністю треба виміряти радіус кола R = 30,5 см і якою кількістю значущих цифр слід обмежитися для числа. щоб площа кола була відома з точністю до 0,1%?
8.6.2. Довжина сторін прямокутника рівні. . Яка допус-тима гранична абсолютна похибка при вимірюванні цих величин однакова для обох сторін, щоб площа S прямокутника можна було визначити з граничною абсолютною похибкою?
1. Що таке абсолютна і відносна похибки?
2. Як класифікуються види помилок?
3. Що означає цифра, вірна в строгому, широкому сенсах?
4. Як знаходиться похибка округленого числа?
5. Як визначити кількість вірних цифр по відносної похибки наближеного числа?
6. Як поширюються абсолютна і відносна похибки в арифметичних діях?
7. Як здійснити оцінку похибки значень елементарних функцій?
8. Як формулюється зворотна задача теорії похибки?
9. Якими мають бути абсолютні похибки аргументів функції, щоб абсолютна похибка функції не перевищувала заданої величини?
В яких випадках використовується метод кордонів?