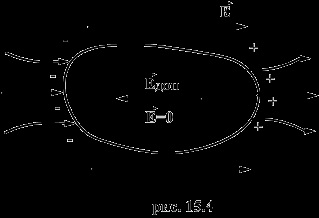
Повідомлений провіднику заряд q розподіляється по його поверхні так, щоб напруженість поля всередині провідника дорівнювала нулю. Якщо провіднику, вже несе заряд q. повідомити ще заряд тієї ж величини, то другий заряд повинен розподілитися по провіднику точно також, як і перший, в іншому випадку він створює в провіднику поле, не рівне нулю. Таким чином, різні за величиною заряди розподіляються на віддаленому від інших тіл (відокремленому) провіднику подібним чином, тобто відношення щільності заряду в двох довільних точках поверхні провідника при будь-якій величині заряду буде один і той же.
Звідси випливає, що потенціал відокремленого провідника пропорційний знаходиться на ньому заряду. Дійсно, збільшення в деяке число раз заряду призводить до збільшення в теж число раз напруженості поля в кожній точці навколишнього провідника простору, тобто
Вводячи відповідний коефіцієнт пропорційності, запишемо або
де С - називається електроємна.
Таким чином, електроємність відокремленого проводнікаесть фізична величина чисельно рівна величині заряду, який необхідно повідомити даному провіднику для збільшення його потенціалу на одиницю. В СІ одиницею ємності є Фарад (Ф).
Визначимо електроємність відокремленого кулі. Потенціал зарядженого кулі радіуса R
Порівнюючи з отримуємо:
11) Конденсатори:
Якщо двом ізольованим один від одного провідників повідомити заряди q1 і q2. то між ними виникає деяка різниця потенціалів Δφ, що залежить від величин зарядів і геометрії провідників. Різниця потенціалів Δφ між двома точками в електричному полі часто називають напругою і позначають буквою U. Найбільший практичний інтерес представляє випадок, коли заряди провідників однакові по модулю і протилежні за знаком: q1 = - q2 = q. В цьому випадку можна ввести понятіеелектріческой ємності.
Електроємна системи з двох провідників називається фізична величина, яка визначається як відношення заряду q одного з провідників до різниці потенціалів Δφ між ними:
В системі СІ одиниця електроємна називається фарад (Ф):
Бувають потрібні такі пристрої, які при невеликому потенціалі накопичували б на себе великі заряди. В основу таких пристроїв, званих конденсаторами. покладено той факт, що ємність провідника зростає при наближенні до нього іншого провідника. Це викликано тим, що під дією поля, створюваного зарядженим провідником, на що знаходиться поблизу незарядженому провідному тілі виникають індуковані заряди. Конденсатори роблять у вигляді двох провідників, називаемихобкладкамі. поміщених близько один до одного. Для того, щоб зовнішні тіла не впливали на ємність конденсатора, обкладкам зраджують таку форму і так мають у своєму розпорядженні їх один щодо одного. щоб поле, створюване що накопичуються на них зарядами. було зосереджено всередині конденсатора.
Кожна із заряджених пластин плоского конденсатора створює поблизу поверхні електричне поле, модуль напруженості якого виражається співвідношенням
Згідно з принципом суперпозиції, напруженість поля, створюваного обома пластинами, дорівнює сумі напряженностейіполей кожної з пластин:
Усередині конденсатора вектора іпараллельни; тому модуль напруженості сумарного поля дорівнює
Поза пластин вектора інаправлени в різні боки, і поетомуE = 0. Поверхнева щільність σ заряду пластин дорівнює q / S, де q - заряд, а S - площа кожної пластини. Різниця потенціалів Δφ між пластинами в однорідному електричному полі дорівнює Ed, де d - відстань між пластинами. З цих співвідношень можна отримати формулу для електроємна плоского конденсатора.
Таким чином, електроємність плоского конденсатора прямо пропорційна площі пластин (обкладок) і обернено пропорційна відстані між ними. Якщо простір між обкладинками заповнене діелектриком, електроємність конденсатора збільшується в ε раз:
Прикладами конденсаторів з іншою конфігурацією обкладок можуть служити сферичний і циліндричний конденсатори. Сферичний конденсатор - це система з двох концентричних проводять сфер радіусів R1 і R2. Циліндричний конденсатор - система з двох співвісних проводять циліндрів радіусів R1 і R2 і довжини L. Ємності цих конденсаторів, заповнених діелектриком з діелектричною проникністю ε, виражаються формулами:
(Сферичний конденсатор), (циліндричний конденсатор).