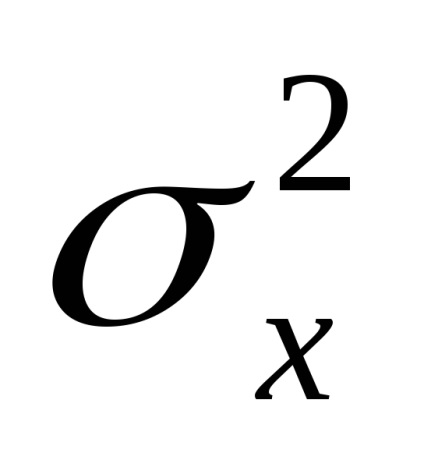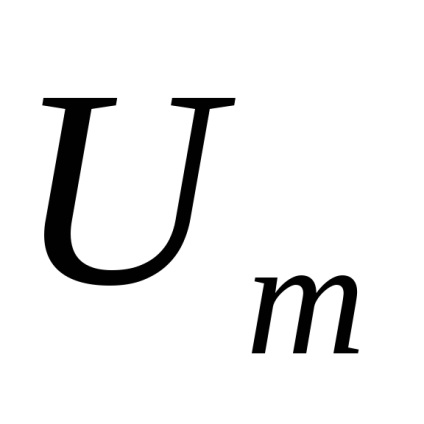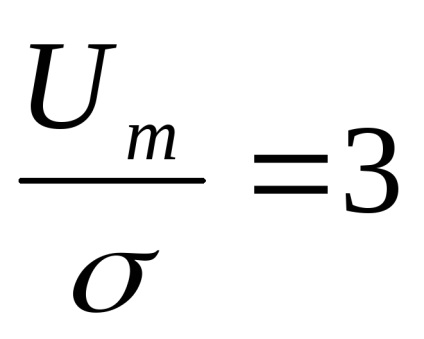стаціонарний випадковий процес з постійною на всіх частотах спектральної щільністю потужності називається білим шумом.
По теоремі Вінера-Хинчина функція кореляції білого шуму:
дорівнює нулю всюди крім точки
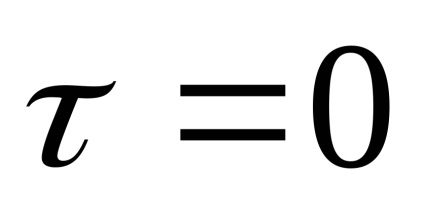
Білий шум є дельта-корельованим процесом. Некоррелірованні миттєвих значень такого випадкового сигналу означає нескінченно велику швидкість зміни їх у часі - як би малий не був інтервал

Білий шум є абстрактною математичною моделлю і відповідає йому фізичний процес, безумовно, не існує в природі. Однак це не заважає приблизно замінювати реальні досить широкосмугові випадкові процеси білим шумом в тих випадках, коли смуга пропускання ланцюга, на яку впливає випадковий сигнал, виявляється істотно вже ефективної ширини спектра шуму.
Б) Гаусове (нормальне) розподіл.
У теорії випадкових сигналів фундаментальне значення має гауссова щільність ймовірності.
містить два числових параметра m і
заміна змінної
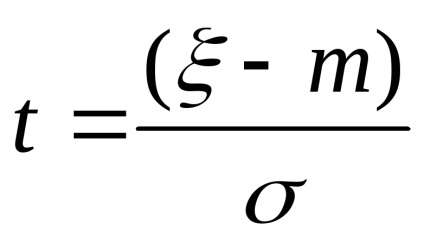
Тут Ф інтеграл ймовірностей
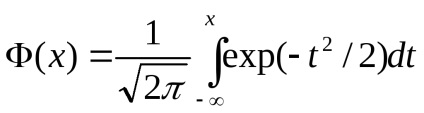
Графік функції F (x) має вигляд монотонної кривої, що змінюється від 0 до 1.
16..Узкополосний випадковий процес. Розподіл Рейлі. Закон Релея-Райса.
Досліджуємо властивості вузькосмугових випадкових сигналів, у яких спектральна щільність потужності має різко виражений максимум поблизу деякої частоти
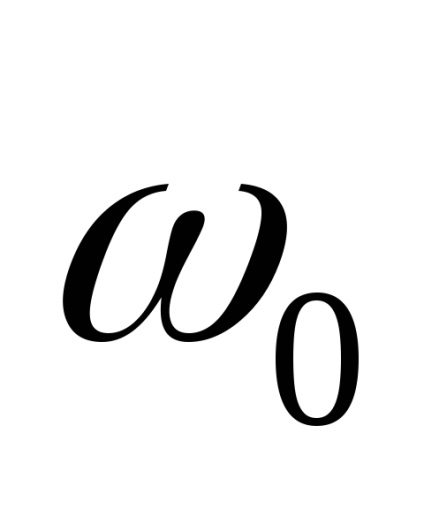
Розглянемо стаціонарний випадковий процес x (t), односторонній спектр потужності якого
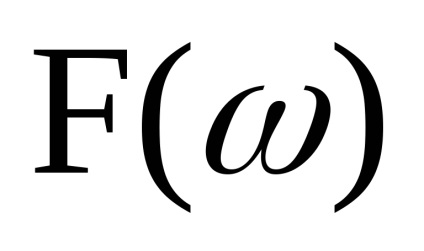
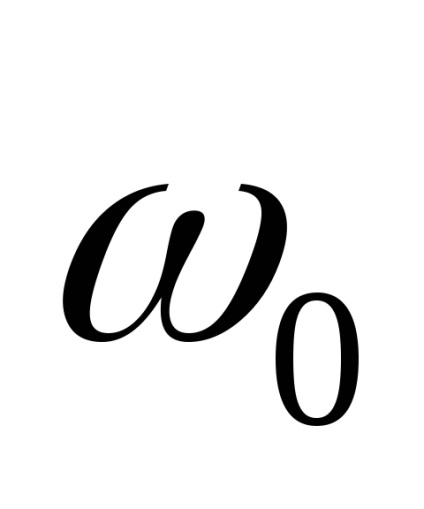
змістимо спектр процесу з околиці частоти
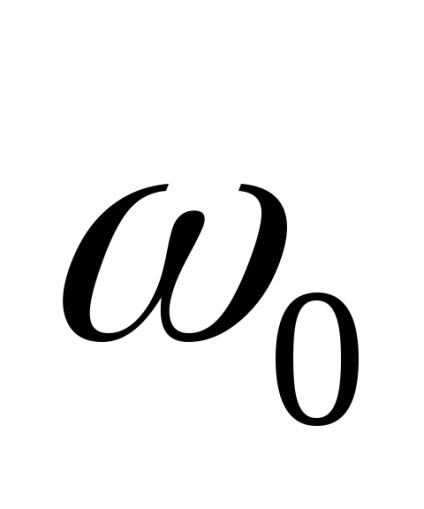
Проводячи усереднення за допомогою щільності ймовірності (7.22) знаходимо середнє значення обвідної і її дисперсію:
Маючи в своєму розпорядженні одновимірної щільністю ймовірності обвідної, можна вирішити ряд завдань теорії вузькосмугових випадкових процесів, зокрема, знайти ймовірність перевищення обвідної деякого заданого рівня.
Випадкові величини, розподілені за законом Релея.
Найпростішою завданням є знаходження одновимірної щільності ймовірності обвідної сумарного коливання. Вважаючи, що корисний сигнал, в той час як шум, запишемо вираз реалізації сумарного процессаX (t). Даний випадковий процес узкополосен, тому його реалізація може бути виражена у вигляді повільно мінливих огібающейU (t) і початкової фази
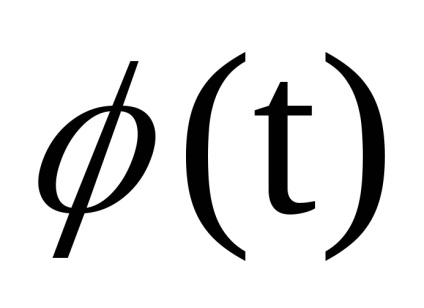
У нових змінних маємо.
Тепер щоб отримати одновимірну щільність ймовірності огинаючої, слід проинтегрировать праву частину формули (7.26) по кутовій координаті в результаті чого знаходимо:
Дана формула виражає закон, який отримав назву закону Райса. Відзначимо, що при
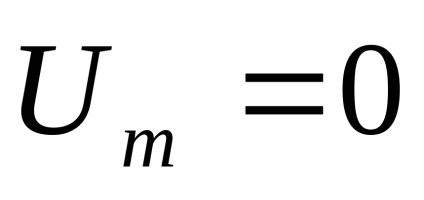
Підставивши цей вираз в (7.27), маємо
Тобто огинає результуючого сигналу розподілена в цьому випадку приблизно нормально з дисперсією