2. Обчислення значень функції z ij = f (x i; y j) у всіх вузлах сітки.
3. Звернення до функції побудови тривимірних графіків.
5.1 Функції plot3d і plot3d1
У Scilab поверхню можна побудувати за допомогою функцій plot3d або plot3d1. Їх відмінність полягає в тому, що plot3d будує поверхню і затоки-
ет її одним кольором, а plot3d1 поверхню, кожна клітинка якої має колір, що залежить від значення функції в кожному відповідному вузлі сітки (див. рис. 5.11).
Звернення до функцій наступне:
5.1. Функції plot3d і plot3d1
тут x вектор-стовпець значень абсцис;
y вектор-стовпець значень ординат;
z матриця значень функції;
theta, alpha дійсні числа, які визначають в градусах сферичні координати кута зору на графік. Попросту кажучи, це кут, під яким спостерігач бачить відображається поверхню;
leg підписи координатних осей графіка символи, відокремлюються знаком @. Наприклад, 'X @ Y @ Z'.
flag масив, що складається з трьох цілочисельних параметрів: [mode, type, box]. тут
mode встановлює колір поверхні (див. табл. 5.1). За замовчуванням дорівнює 2 колір заливки синій, прямокутна сітка виводиться.
Таблиця 5.1. Значення параметра mode
> 0 поверхня має колір ¾mode¿, виводиться прямокутна сітка
0 виводиться прямокутна сітка, заливка відсутня (білий колір)
<0 поверхность имеет цвет ¾mode¿, отсутствует прямоугольная сетка
type дозволяє управляти масштабом графіка (див. табл. 5.2), за замовчуванням має значення 2;
(Див. Табл. 5.3). За замовчуванням дорівнює 4.
ebox визначає межі області, в яку буде виводитися поверхню, як вектор [xmin, xmax, ymin, ymax, zmin, zmax]. Цей параметр може використовуватися тільки при значенні параметра type = 1.
keyn = valuen послідовність значень властивостей графіка key1 = value1, key2 = value2. keyn = valuen,
таких як товщина лінії, її колір, колір заливки фону графічного вікна, наявність маркера і ін. (див. параграф 4.6).
Таким чином, функції plot3d (plot3d1) в якості параметрів необхідно передати прямокутну сітку і матрицю значень у вузлах сітки.
Побудувати графік функції Z = sin (t) cos (t).
Створимо масив значень аргументу t. Обчислимо значення функції і запишемо їх в масив Z.
Зверніть увагу, що при зверненні до функції plot3d в якості параметрів X і Y. задають прямокутну сітку, двічі вказано параметр t, оскільки обидві функції і sin, і cos залежать від однієї змінної t (див. Лістинг 5.1, рис.5.1).
Лістинг 5.1. Побудова графіка функції Z = sin (t) cos (t) за допомогою функції plot3d
Тепер трохи ускладнити завдання. Побудуємо поверхню, рівняння якої задається двома незалежними змінними.
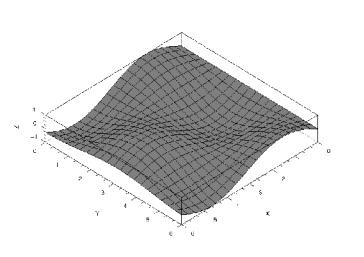
Побудувати графік функції Z = 5y 2 x 2.
5.1. Функції plot3d і plot3d1
Мал. 5.1. Графік функції Z = sin (t) cos (t)
Перш за все поставимо масиви X і Y.
Потім сформуємо матрицю значень функції Z (x i; y j), використовуючи оператор циклу for. Тут i параметр циклу, який буде перебирати всі значення масиву X, а j параметр циклу, який буде зіставляти кожному значенню масиву X по черзі всі значення масиву Y.
Таким чином, спочатку будуть обчислені всі значення функції Z при мінливому Y (від першого до останнього значення в масиві) і першому значенні масиву X. Потім при другому значенні масиву X і т. Д.
Нагадаємо, тут length визначає кількість елементів масиву X (Y) (див. Розділ 2).
Нарешті, для побудови поверхні звернемося до функції plot3d1 (див. Ли
Стінг 5.2, рис.5.12).
Як видно з прикладу, використання лише функції plot3d для графічного зображення показників, що залежать від двох незалежних змінних, досить складно. У Scilab існує кілька команд, покликаних полегшити процедуру створення прямокутної сітки це genfac3d і eval3dp.
Найпростішою з них по синтаксису є функція genfac3d:
Тут xx, yy, zz результуюча матриця розміром (4; n 1 m 1), де xx (:, i), yy (:, i) і zz (:, i) координати кожної з осередків прямокутної сітки;
x вектор x-координат розміру m;
y вектор y-координат розміру n;
z матриця розміру (m; n) значень функції Z (x i; y j).
Побудувати графік функції Z = sin (t) cos (t).
Визначимо масив параметра t і обчислимо значення функції Z = sin (t) cos (t). Прямокутну сітку створимо за допомогою команди genfac3d (див. Лістинг 5.3).
Лістинг 5.3. Створення прямокутної сітки графіка командою genfac3d і побудова її графіка за допомогою функції plot3d
Для формування графіка звернемося до функції plot3d (див. Рис. 5.1). Недоліком команди genfac3d є те, що вона все-таки не спрощує
роботу з функцією plot3d, якщо поверхня задається функцією від двох змінних. В такому випадку необхідно використовувати команду eval3dp:
Xf, Yf, Zf - результуюча матриця розміром (4; n 1 m 1), де xx (:, i), yy (:, i) і zz (:, i) координати кожної з осередків прямокутної сітки;
fun функція, певна користувачем, яка задає тривимірний графік;
5.1. Функції plot3d і plot3d1
p1 вектор розміру m;
p2 вектор розміру n.
Проілюструємо дію команди eval3dp наступним прикладом.
Побудувати графік, заданий наступними рівняннями: x = p 1 sin (p 1) cos (p 2), y = p 1 cos (p 1) cos (p 2), z = p 1 sin (p 2).
Перш за все, визначимо масиви значень параметрів p 1 і p 2. Далі створимо функцію scp, яка задає графік.
Нагадаємо, що функції в Scilab створюються за допомогою команди deff:
де s1, s2. список вихідних параметрів, тобто змінних, яким буде присвоєно кінцевий результат обчислень;
newfunction ім'я створюваної функції, воно буде використовуватися для її виклику;
e1, e2. вхідні параметри.
Зверніть увагу, що команда deff записана в три рядки тільки для зручності читання лістингу (див. Лістинг 5.4).
Лістинг 5.4. Створення прямокутної сітки графіка командою eval3dp і побудова її графіка за допомогою функції plot3d
p2 = linspace (0,2 *% pi, 10); deff ( "[x, y, z] = scp (p1, p2)", [ "x = p1. * sin (p1). * cos (p2)"; "y = p1. * cos (p1). * cos (p2) ";
"Z = p1. * Sin (p2)"]); [Xf, Yf, Zf] = eval3dp (scp, p1, p2); plot3d (Xf, Yf, Zf);
Тепер сформуємо прямокутну мережу за допомогою команди eval3dp і побудуємо графік, звернувшись до функції plot3d (див. Рис. 5.13).